基于 RP2040 和 TMF8821 传感器的无接触式手势控制游戏
项目介绍
本项目基于 Raspberry Pi Pico (RP2040) 微控制器和 TMF8821 dToF传感器开发了一款无接触手势控制游戏。游戏通过检测手掌位置和移动方向来实现菜单导航和游戏交互,玩家无需触摸屏幕,只需在传感器上方移动手掌即可控制游戏。游戏具有菜单系统、难度设置和实时反馈功能,为用户提供了创新的交互体验。
硬件介绍
项目使用了以下核心硬件组件:
树莓派RP2040游戏机: 双核 Arm Cortex-M0+ 处理器,运行频率高达 133 MHz,512KB FLASH 存储和 264KB RAM,支持多核编程,其中ST7789驱动的240x240 像素的彩色显示屏,用于显示游戏界面和交互元素。
TMF8821 ToF 传感器模块: 高精度距离传感器,能够测量物体距离并检测简单的手势动作,测量范围可达 2m。
电路连接:
- SPI 接口连接显示屏 (TX: GPIO3, SCK: GPIO2, DC: GPIO1, RESET: GPIO0)
- I2C 接口连接 ToF 传感器
- LED 指示灯 (GPIO4)
方案框图和设计思路
系统架构图

设计思路
- 双核协同工作,Core0 负责游戏逻辑计算、UI 渲染和用户交互。Core1 专门处理传感器数据的获取和初步处理,包括手势识别。
- 通过互斥锁和共享内存实现核间通信,使用互斥锁确保数据一致性和线程安全。
- 游戏状态机设计:
- 菜单状态 (STATE_MENU)
- 配置状态 (STATE_CONFIG)
- 游戏状态 (STATE_GAME)
- 游戏结束状态 (STATE_GAME_OVER)
- 手势和高度控制系统:识别上、下、左、右四个基本方向的手势以及高度信息。
软件流程图和关键代码
主要程序流程图
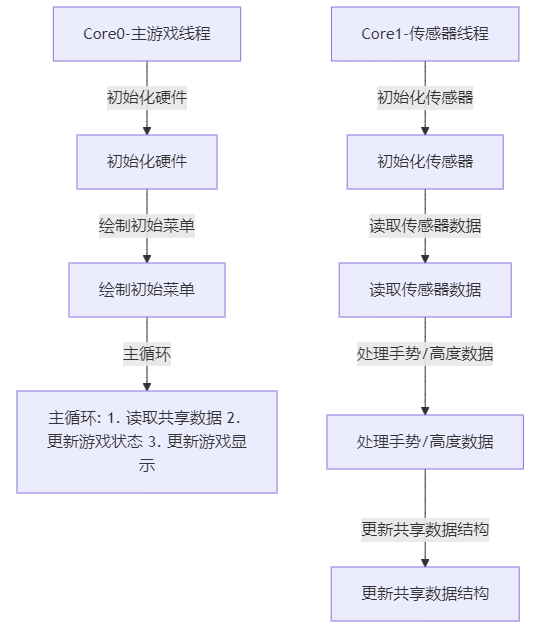
关键代码解析
1. 双核通信机制
这段代码实现了双核间的安全通信。Core1 负责从传感器获取数据并更新共享数据结构,Core0 从共享结构中读取数据用于更新游戏状态。互斥锁确保在一个核心访问数据时,另一个核心不会同时修改数据,避免了数据竞争问题。
// 共享数据结构
struct SharedDirection {
mutex_t mutex;
bool new_data_available;
char direction;
};
// 更新共享方向数据
void update_shared_direction(char direction) {
mutex_enter_blocking(&shared_direction.mutex);
shared_direction.direction = direction;
shared_direction.new_data_available = true;
mutex_exit(&shared_direction.mutex);
}
// 获取共享方向数据
char get_shared_direction(bool *new_data) {
char direction;
mutex_enter_blocking(&shared_direction.mutex);
direction = shared_direction.direction;
if (new_data) {
*new_data = shared_direction.new_data_available;
shared_direction.new_data_available = false;
}
mutex_exit(&shared_direction.mutex);
return direction;
}
2. 手势方向处理和防抖动
TMF8821传感器提供了3 * 3 (也可以配置成 3 * 6 或者 4 * 4)的矩阵式深度信息。将处理后的数据传到电脑上,并进行可视化处理,可以直观地感受到随着手势的变化,传感器的深度信息也随之变化,并且准确性和实时性都很好。

下面是手势识别的核心算法,用于从多个时间帧的传感器数据中检测手的移动方向:
char determine_direction(std::deque<std::pair<std::vector<uint16_t>, std::vector<uint8_t>>> &buffer) {
if (buffer.size() < 3) {
return '-';
}
// 只考虑100mm距离内的物体进行方向检测
const int max_distance_for_direction = 100;
std::vector<std::pair<float, float>> centroids;
for (const auto &frame : buffer) {
const auto &distances = frame.first;
std::vector<float> x_coords, y_coords;
for (size_t i = 0; i < distances.size(); ++i) {
// 只考虑在最大距离阈值内的点
if (distances[i] > 0 && distances[i] <= max_distance_for_direction) {
x_coords.push_back(i % 3); // 计算在3x3网格中的x坐标
y_coords.push_back(i / 3); // 计算在3x3网格中的y坐标
}
}
if (!x_coords.empty() && !y_coords.empty()) {
// 计算当前帧中有效点的质心
float g_x = std::accumulate(x_coords.begin(), x_coords.end(), 0.0f) / x_coords.size();
float g_y = std::accumulate(y_coords.begin(), y_coords.end(), 0.0f) / y_coords.size();
centroids.emplace_back(g_x, g_y);
}
}
// 如果没有足够的有效质心(近距离物体),返回无方向
if (centroids.size() < 3) {
return '-';
}
// 创建索引数组,用于线性回归
std::vector<float> indices(centroids.size());
std::iota(indices.begin(), indices.end(), 0); // 填充0,1,2,...
// 计算质心x坐标的平均值和索引的平均值
float x_mean = std::accumulate(indices.begin(), indices.end(), 0.0f) / indices.size();
float y_mean = std::accumulate(centroids.begin(), centroids.end(), 0.0f,
[](float sum, const std::pair<float, float>& p) {
return sum + p.first;
}) / centroids.size();
// 计算x方向的线性回归斜率
// 斜率公式: sum((x_i - x_mean) * (y_i - y_mean)) / sum((x_i - x_mean)^2)
float x_slope = std::inner_product(
indices.begin(), indices.end(), centroids.begin(), 0.0f,
std::plus<>(),
[x_mean, y_mean](float a, const std::pair<float, float> &b) {
return (a - x_mean) * (b.first - y_mean);
}
) / std::inner_product(
indices.begin(), indices.end(), indices.begin(), 0.0f,
std::plus<>(),
[x_mean](float a, float b) {
return (a - x_mean) * (b - x_mean);
}
);
// 计算y坐标的平均值
y_mean = std::accumulate(centroids.begin(), centroids.end(), 0.0f,
[](float sum, const std::pair<float, float>& p) {
return sum + p.second;
}) / centroids.size();
// 计算y方向的线性回归斜率
float y_slope = std::inner_product(
indices.begin(), indices.end(), centroids.begin(), 0.0f,
std::plus<>(),
[x_mean, y_mean](float a, const std::pair<float, float> &b) {
return (a - x_mean) * (b.second - y_mean);
}
) / std::inner_product(
indices.begin(), indices.end(), indices.begin(), 0.0f,
std::plus<>(),
[x_mean](float a, float b) {
return (a - x_mean) * (b - x_mean);
}
);
// 根据斜率获取方向字符,并应用方向过滤器
char new_arrow = get_arrow(x_slope, y_slope);
char filtered_arrow = direction_filter.update(new_arrow);
return filtered_arrow;
}
详细解析如下:
1. 输入数据结构:
- buffer 是一个双端队列,存储了多个时间帧的传感器数据
- 每个时间帧包含一对向量:距离数据和置信度数据
- 距离数据表示距离物体的距离(毫米),置信度数据表示测量的可靠性
2. 算法流程:
- 距离数据表示距离物体的距离(毫米),置信度数据表示测量的可靠性
- 确保缓冲区至少有3个时间帧,否则无法可靠检测方向
- 对每一帧,找出距离小于100mm的点(近距离物体),计算这些点在3x3网格中的坐标,然后计算这些点的平均位置(质心),将每一帧的质心存入centroids向量
- 创建与质心数量相等的索引数组,表示时间序列对质心坐标进行线性回归分析,计算x和y方向的变化率(斜率)。x_slope表示物体在x方向上的移动趋势(正值表示向右移动,负值表示向左移动),y_slope表示物体在y方向上的移动趋势(正值表示向下移动,负值表示向上移动)。
- 根据x_slope和y_slope的值和大小关系,确定主要移动方向。通过get_arrow函数将斜率转换为方向字符:'u'上、'd'下、'l'左、'r'右。使用direction_filter过滤器对方向进行平滑处理,消除偶发的方向变化。
- 最终演示效果如下:
3. 线性回归算法的详细解释
- 数据准备阶段(以取3帧数据为例):
- 取最近3帧的有效数据(距离≤100mm的点)
- 对每帧计算质心坐标(x,y),形成时间序列数据:
帧0 → (x0,y0)
帧1 → (x1,y1)
帧2 → (x2,y2)
- 线性回归数学模型:
- 建立时间t与坐标的线性关系:
x(t) = a_x * t + b_x
y(t) = a_y * t + b_y - 其中t∈{0,1,2}表示帧序号,a_x和a_y即为回归斜率
- 建立时间t与坐标的线性关系:
- 斜率计算公式(以x方向为例):
a_x = [Σ(t - t̄)(x_t - x̄)] / [Σ(t - t̄)^2]
- 分子:时间与坐标的协方差
- 分母:时间的方差
功能展示图及说明
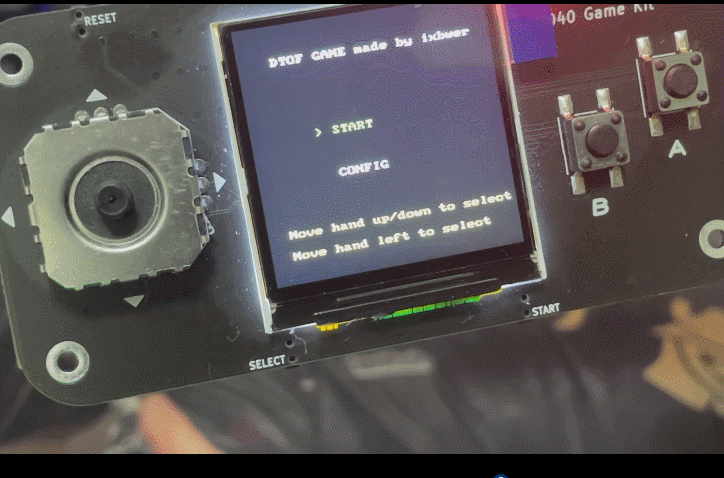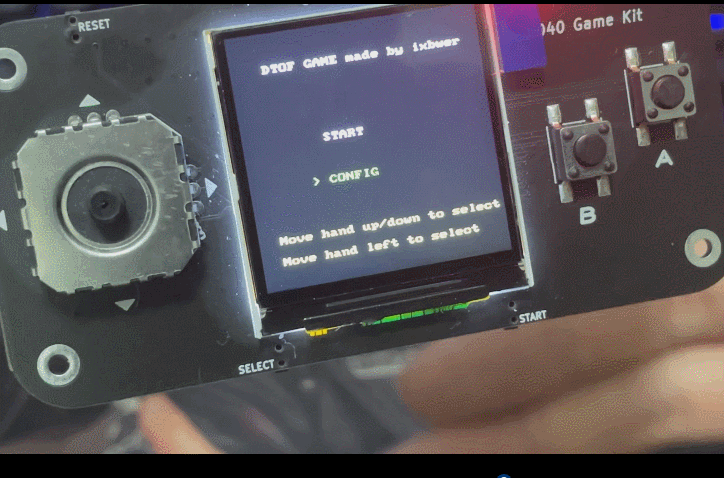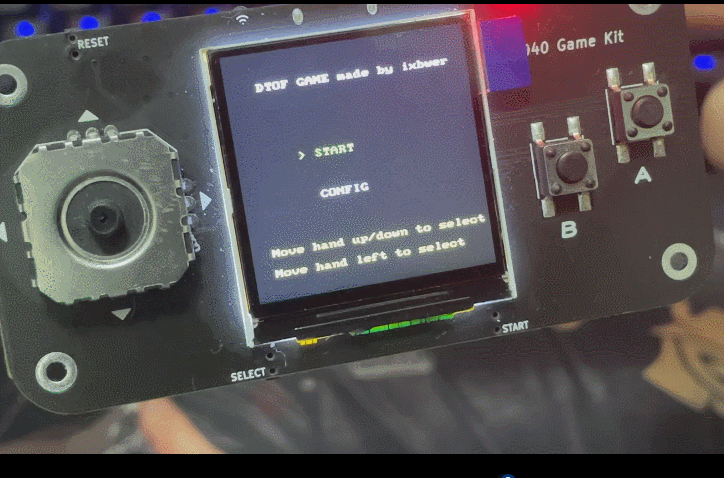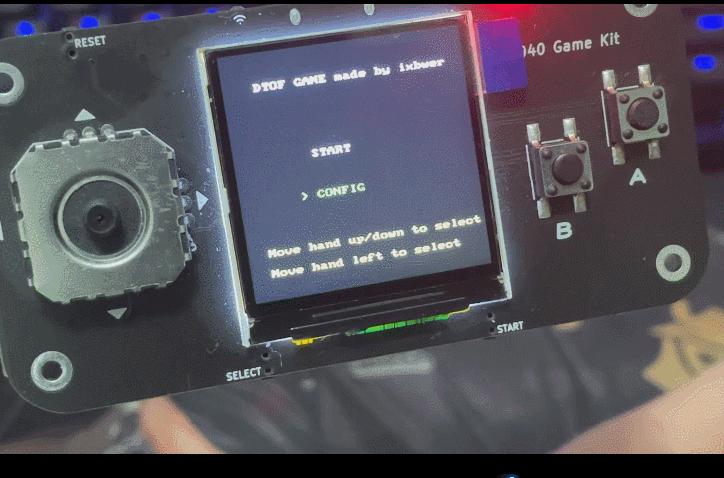
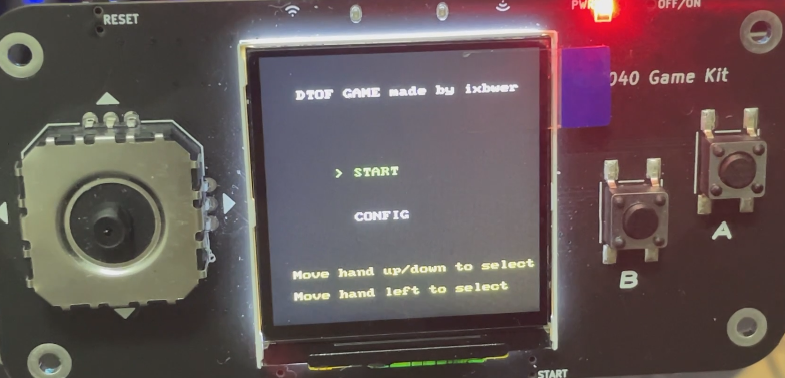
1. 主菜单界面
- 显示游戏标题 "DTOF GAME made by ixbwer"
- 提供 "START" 和 "CONFIG" 两个选项
- 当前选中的选项用绿色高亮显示
- 底部显示控制说明
2. 配置界面
- 显示难度设置选项:EASY、MEDIUM、HARD
- 当前选中的难度用绿色高亮显示
- 不同难度对应不同的游戏速度和挑战性

3. 游戏界面
- 显示当前得分和难度级别
- 两条交互条:一条表示传感器测量的手部高度,另一条随机上下移动,移动的速度根据游戏难度的上升而加快
- 显示匹配进度条:当两个高度匹配时为绿色,不匹配时为红色
- 底部显示游戏剩余能量条,如果能量条为0,则游戏结束

4. 游戏结束界面
- 显示 "GAME OVER" 和最终得分
- 提供 "RESTART" 和 "MENU" 两个选项

项目中遇到的难题和解决方法
1. 传感器数据稳定性问题
ToF 传感器数据存在噪声和不稳定性,导致手势识别不准确。
解决方法:
实现了数据平滑处理算法和防抖动机制
2. 多核编程协调问题
两个核心同时访问共享数据结构导致数据不一致和竞争条件。
解决方法:
使用互斥锁机制保护共享数据的访问
4. 手势识别精度
简单的阈值判断难以准确识别手势方向。
解决方法:
- 优化了传感器数据处理算法
- 增加了手势确认机制,减少误判
- 调整了手势敏感度,使控制更加自然
心得体会
项目收获
通过本项目深入了解了基于 RP2040 的嵌入式系统开发,包括多核编程、外设控制和实时系统设计,掌握了 ToF 传感器的工作原理和应用方法,特别是在手势识别方面的实现技巧。同时也学习了使用互斥锁和共享内存实现多核间通信的方法。
无接触交互作为一种新型人机交互方式,不仅在游戏领域有着巨大潜力,在医疗、公共设施等对卫生要求高的场景也有重要应用价值。随着对TMF8821芯片的不断深入了解,我已经可以想象到这类芯片在医疗、工业、消费电子领域拥有的无限前景。
改进建议
未来可以考虑结合多种传感器(如加速度计、陀螺仪)提高手势识别的精度和丰富度。如果dToF的分辨率更高,可以引入机器学习算法提高手势识别的准确性,支持更复杂的手势交互。
其他
项目代码:https://github.com/ixbwer/rp2040-tmf8821