1 项目介绍

本项目采用TMF8821距离传感器和RP2040微控制器作为核心硬件，通过采集平面上多个点的距离数据，实现平面角度的测量和平面距离的计算。以下是项目的主要特点：

1. 高精度：采用TMF8821传感器，具有毫米级测量精度，确保了测量结果的准确性。
2. 灵活性：可根据实际需求，调整测量点的数量和位置，适应不同场景的测量需求。
3. 易操作：采用图形化界面，操作简便，易于上手。
4. 便携性强：系统体积小巧，便于携带，适用于现场测量。

平面角度测量：通过采集平面上多个点的距离数据，计算得到平面与测量点之间的角度。

平面距离计算：根据测量点与平面之间的距离数据，以及平面的法向量，计算得到平面距离。

实时显示：测量结果实时显示在液晶显示屏上，便于用户查看。

本项目可广泛应用于以下领域：

1. 建筑行业：用于测量建筑物的平面角度和距离，提高施工精度。
2. 工业制造：用于检测生产线上的产品尺寸，确保产品质量。
3. 科研实验：为各类科研实验提供精确的测量数据。
4. 其他领域：如地质勘探、考古挖掘等，均可应用于平面角度和距离的测量。

2 开发设计

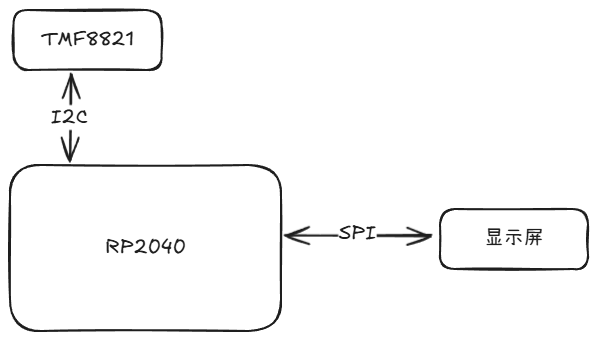
TMF8821基础介绍

工作原理

TMF8821的工作原理使用由迭代设置定义的VCSEL垂直腔面发射激光器脉冲序列。这些脉冲使用MLA（微透镜阵列）来照亮FoI（照明场）。一个物体将这些光线反射回TMF8821接收机光学透镜上，并反射到一个SPAD（单光子雪崩探测器）阵列上。

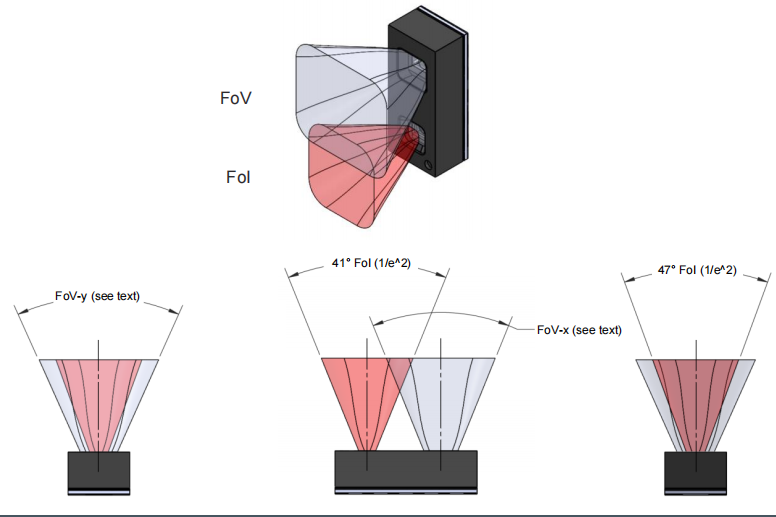
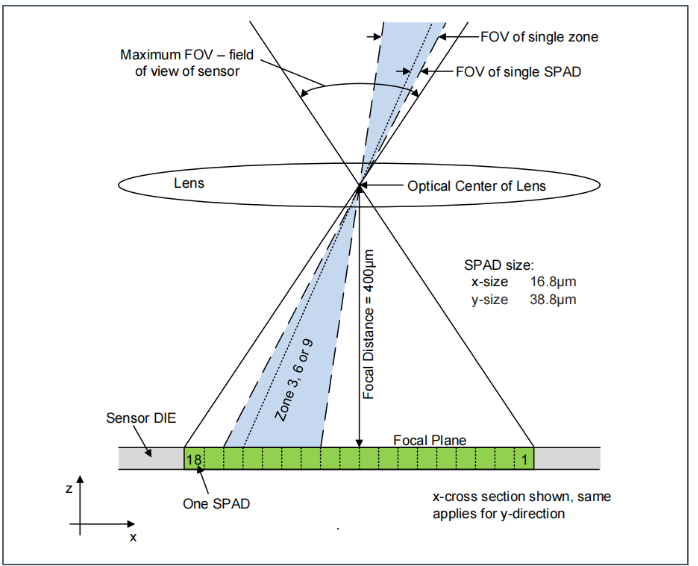
分区越多迭代次数越多，测量等待时间越长。

I²C接口

默认地址0x41

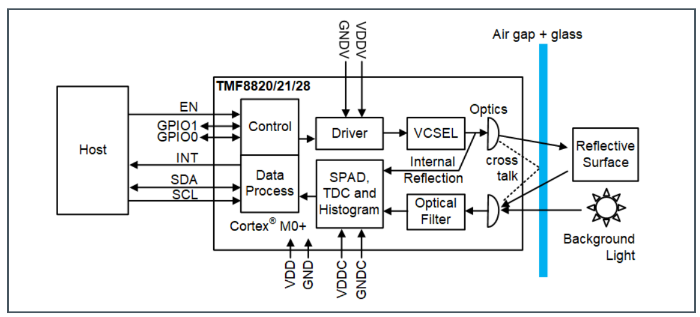
配置好引脚，并拉高EN

通过寄存器读取到0x00地址为 0x80 Bootloader running

调试学习

利用官方的PYTHON 和ARDUINO驱动，在上位机上做了一个9宫格界面。

后续需要确认9宫格的位置是否正确。

二、开发设计

原理

测量使用了 dTOF（直接时间飞行） 激光传感器，并且测量是在一个 3x3的模式 下进行的，得到的 9个距离值。从这些距离值中，我们需要求解 平面与测量点之间的角度。因此需要计算平面的 法向量，然后基于法向量与测量点之间的相对位置来求解角度。

关键步骤：

理解测量数据：

你的测量数据给出了 9个距离值，假设这些值是从 测量点 到平面上 9个不同点的距离。这些点构成了一个3x3的网格。

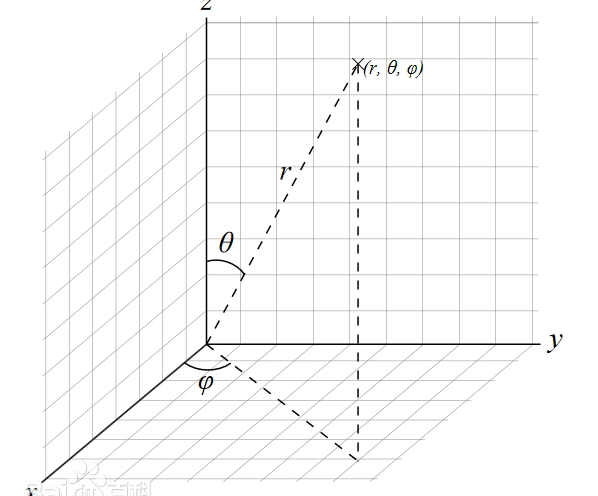
将极坐标到笛卡尔坐标的转换公式，得到网格上的9个点的坐标为 (x_i, y_i, z_i)。可以根据这些点的坐标计算平面方程。

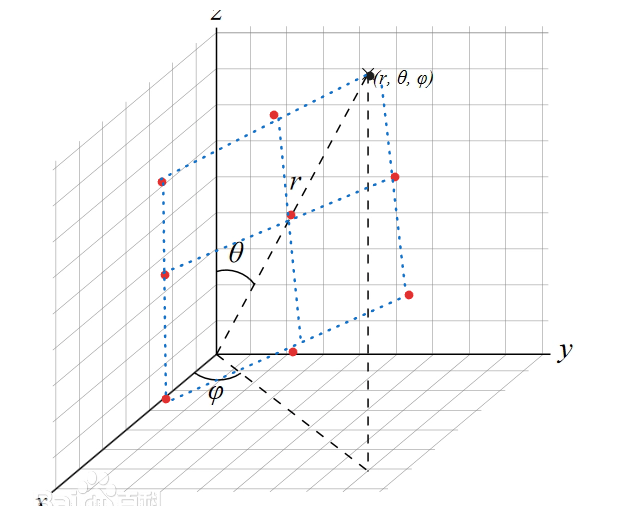
平面方程和法向量：

通过已知的 9个点的笛卡尔坐标点，我们可以估算出平面上的3个点的坐标。

利用这3个点，我们可以计算出平面的 法向量。

三、代码展示

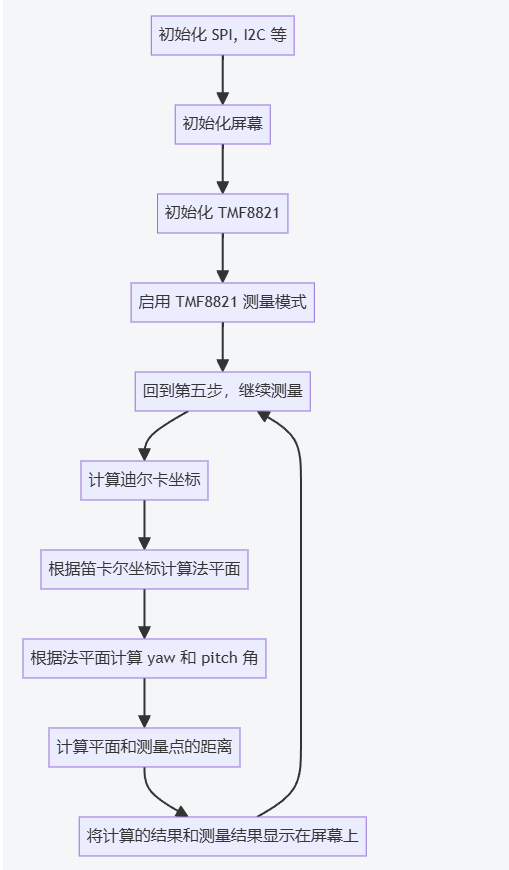
1. 初始化 SPI 和 I2C: 这一部分表示初始化外设接口，如SPI和I2C。
2. 初始化屏幕: 配置显示屏以便后续显示数据。
3. 初始化 TMF8821: 配置和初始化 TMF8821 传感器，确保其可以进行测量。
4. 启用 TMF8821 测量模式: 设置传感器进入测量模式，准备采集数据。
5. 采集 TMF8821 测量数据: 获取传感器的测量结果，通常是9个测量点。
6. 计算迪尔卡坐标: 根据9个点的极坐标数据，转换为笛卡尔坐标系中的数据。
7. 根据笛卡尔坐标计算法平面: 使用笛卡尔坐标计算法平面方程。
8. 计算 yaw 和 pitch 角: 通过法平面数据计算出俯仰角（pitch）和偏航角（yaw）。
9. 计算平面和测量点的距离: 根据法平面方程和测量点计算出平面到测量点的距离。
10. 将计算的结果显示在屏幕上: 显示计算的结果和测量结果。
11. 回到第五步: 继续进行下一轮数据采集和计算。

import uos
import test.st7789 as st7789
from test.fonts import vga2_8x8 as font1
from test.fonts import vga1_16x32 as font2
import random
import framebuf
from machine import Pin, SPI, ADC,PWM
import time, math,array
from utime import sleep_ms
from test.buzzer_music import music
from test import mma7660
import struct
from image_data import *
from tmf8828 import *
import math
# import numpy as np
from plane_info_and_distance import *
song='0 B4 1 43 0.6456692814826965;2 B4 1 43 0.7716535329818726;3 A4 1 43 0.8661417365074158;5 B4 1 43 0.9370078444480896;7 D5 1 43;9 B4 1 43;11 F#4 1 43;12 A4 2 43;14 B4 1 43;16 B4 1 43;18 B4 1 43;19 A4 1 43;21 B4 1 43;23 F5 1 43;25 E5 1 43;27 D5 1 43;28 A4 2 43;30 B4 1 43;32 B4 1 43;34 B4 1 43;35 A4 1 43;37 B4 1 43;39 D5 1 43;41 B4 1 43;43 F#4 1 43;44 A4 2 43;46 B4 1 43;48 B4 1 43;50 B4 1 43;52 A4 1 43;53 B4 1 43;62 B4 1 43;64 B4 1 43;66 B4 1 43;67 A4 1 43;69 B4 1 43;71 D5 1 43;73 B4 1 43;75 F#4 1 43;76 A4 2 43;78 B4 1 43;80 B4 1 43;82 B4 1 43;83 A4 1 43;85 B4 1 43;87 F5 1 43;89 E5 1 43;91 D5 1 43;92 A4 2 43;94 B4 1 43;96 B4 1 43;98 B4 1 43;99 A4 1 43;101 B4 1 43;103 D5 1 43;105 B4 1 43;107 F#4 1 43;108 A4 2 43;110 B4 1 43;112 B4 1 43;114 B4 1 43;115 A4 1 43;117 B4 1 43;119 F5 1 43;121 E5 1 43;123 D5 1 43;124 A4 2 43;126 B4 1 43;128 B4 1 43;130 B4 1 43;131 A4 1 43;133 B4 1 43;135 D5 1 43;137 B4 1 43;139 F#4 1 43;140 A4 2 43;142 B4 1 43;144 B4 1 43;146 B4 1 43;147 A4 1 43;149 B4 1 43;151 F5 1 43;153 E5 1 43;155 D5 1 43;156 A4 2 43;158 B4 1 43;160 B4 1 43;162 B4 1 43;163 A4 1 43;165 B4 1 43;167 D5 1 43;169 B4 1 43;171 F#4 1 43;172 A4 2 43;174 B4 1 43;176 B4 1 43;178 B4 1 43;179 A4 1 43;180 B4 1 43;181 D5 1 43;183 F5 1 43;185 E5 1 43;187 D5 1 43;188 A4 2 43'
pwm = PWM(Pin(19))
mySong = music(song, pins=[Pin(23)])
pwm.freq(50)
#image_file0 = "/logo.bin" #图片文件地址
st7789_res = 0
st7789_dc  = 1
disp_width = 240
disp_height = 240
CENTER_Y = int(disp_width/2)
CENTER_X = int(disp_height/2)
spi_sck=Pin(2)
spi_tx=Pin(3)
spi0=SPI(0,baudrate=4000000, phase=1, polarity=1, sck=spi_sck, mosi=spi_tx)
sda=Pin(10)
scl=Pin(11)
mma7660=machine.I2C(1,sda=sda,scl=scl,freq=400000)
mma7660.writeto_mem(76,7,b'1')

display = st7789.ST7789(spi0, disp_width, disp_width,
                          reset=machine.Pin(st7789_res, machine.Pin.OUT),
                          dc=machine.Pin(st7789_dc, machine.Pin.OUT),
                          xstart=0, ystart=0, rotation=0)
display.fill(st7789.BLACK)
# display.text(font2, "EETREE", 10, 10)
# display.text(font2, "www.eetree.cn", 10, 40)
xAxis = ADC(Pin(28))
yAxis = ADC(Pin(29))
buttonB = Pin(5,Pin.IN, Pin.PULL_UP) #B
buttonA = Pin(6,Pin.IN, Pin.PULL_UP) #A
buttonStart = Pin(7,Pin.IN, Pin.PULL_UP) #A
buttonSelect = Pin(8,Pin.IN, Pin.PULL_UP) #A

t=0
##########################################TMF8821 #########################################

global log

log=0

tm8821 = I2C(0, scl=Pin(17), sda=Pin(16),freq=400000)  # 根据你的硬件连接配置适当的 SCL 和 SDA 引脚

ENABLE = Pin(22, Pin.OUT)

INIT_MESSURE(tm8821,tmf8828_image,tmf8828_image_length,ENABLE)

distances=[1,2,3,4,5,6,7,8,9]

distances_buf = [distances] * 10  # 这里用的是复制操作，distances_buf 会包含 10 个相同的 distances 列表

distances_pre = [0,0,0,0,0,0,0,0,0]

tft=display

mode= 0

##########################################TMF8821 #########################################


# 绘制3D坐标系

def draw_3d_axes(tft):

    tft.line(40, 160, 40, 20, st7789.RED)

    tft.line(40, 160, 20, 220, st7789.GREEN)

    tft.line(40, 160, 220, 160, st7789.BLUE)

draw_3d_axes(tft)

def switch_case(value,distances):

    P = points_cartesian_3d(distances)

    n1 = norm(normal_vector(P[0], P[2], P[6]))

    n2 = norm(normal_vector(P[0], P[2], P[8]))

    n3 = norm(normal_vector(P[0], P[6], P[8]))

    n4 = norm(normal_vector(P[2], P[6], P[8]))

    return norm((n1 + n2 + n3 + n4)),P

def drawPlant(distances):
    n,P= switch_case(mode,distances)
    dis =plane_distance_to_origin(n[0],n[1],n[2],P[4][0],P[4][1],P[4][2])
    pitch_deg, yaw_deg = calculate_angles(n[0],n[1],n[2])

    display.text(font1, "yaw= %02f" %(yaw_deg) , 20 ,  20)

    display.text(font1, "pitch=%02f" %(pitch_deg) , 20 ,  160)

    display.text(font1, "dist=%04d" %(dis) , 20 ,  60)

    display.text(font1, "mode=%d" %(mode) , 20 ,  220)

newdis =0
olddis =0
TIMECOUNT=0
while True:
    TIMECOUNT+=1
    if TIMECOUNT>1:
        drawPlant(distances)
        TIMECOUNT =0
    distances=readdistance(tm8821,distances)
    #根据主控显示器
    for i in range(3):
        display.text(font1, "%04d" %(distances[i*3]) , 40 +i*80 ,  40)
        display.text(font1, "%04d" %(distances[i*3+1]) ,40+ i*80 ,  120)
        display.text(font1, "%04d" %(distances[i*3+2]) ,40+ i*80 , 200)

# import numpy as np
import math
# 三维极坐标转换为笛卡尔坐标

def polar_to_cartesian_3d(r, theta, phi):
    # 将角度转换为弧度
    theta_rad = math.radians(theta)
    phi_rad = math.radians(phi)
    # 计算笛卡尔坐标
    x = r * math.sin(phi_rad) * math.cos(theta_rad)
    y = r * math.sin(phi_rad) * math.sin(theta_rad)
    z = r * math.cos(phi_rad)
    return x, y, z

# 计算所有点的三维笛卡尔坐标

def points_cartesian_3d(distance):

    points_polar_3d=[[0] * 3 for _ in range(9)]

    points_polar_3d[0]=[distance[0],180-21.6/2,90-22/2]

    points_polar_3d[3]=[distance[3],180+0,90-22/2]

    points_polar_3d[6]=[distance[6],180+21.6/2,90-22/2]

    points_polar_3d[1]=[distance[1],180-21.6/2,90-0]

    points_polar_3d[4]=[distance[4],180+0,90-0]

    points_polar_3d[7]=[distance[7],180+21.6/2,90-0]

    points_polar_3d[2]=[distance[2],180+-21.6/2,90+22/2]

    points_polar_3d[5]=[distance[5],180+0,90+22/2]

    points_polar_3d[8]=[distance[8],180+21.6/2,90-22/2]

    points_cartesian_3d = []
    for i, (r, theta, phi) in enumerate(points_polar_3d, 1):
        # 计算三维笛卡尔坐标
        x, y, z = polar_to_cartesian_3d(r, theta, phi)
        points_cartesian_3d.append((x, y, z))
    return points_cartesian_3d

def cross_product(v1, v2):
    # 计算两个向量的叉积
    return [
        v1[1] * v2[2] - v1[2] * v2[1],  # x
        v1[2] * v2[0] - v1[0] * v2[2],  # y
        v1[0] * v2[1] - v1[1] * v2[0]   # z
    ]

def vector_subtract(p1, p2):
    # 计算向量 P1P2 = (x2 - x1, y2 - y1, z2 - z1)
    return [p2[0] - p1[0], p2[1] - p1[1], p2[2] - p1[2]]


def normal_vector(p1, p2, p3):
    # 计算法向量
    v1 = vector_subtract(p1, p2)
    v2 = vector_subtract(p1, p3)
    return cross_product(v1, v2)

def norm(vector):
    magnitude = math.sqrt(vector[0]**2 + vector[1]**2 + vector[2]**2)
    if(magnitude == 0):
        magnitude=1
    # 归一化向量
    normalized_vector = [vector[0] / magnitude, vector[1] / magnitude, vector[2] / magnitude]
    return normalized_vector

def calculate_angles(Nx, Ny, Nz):

    # 计算俯仰角 (Pitch)

    pitch = math.atan2(Nz, math.sqrt(Nx**2 + Ny**2))  # arctan(Nz / sqrt(Nx^2 + Ny^2))

    # 计算横摆角 (Yaw) / 偏航角 (Yaw)
    yaw = math.atan2(Ny, Nx)  # arctan(Ny / Nx)
    # 转换为角度（度）
    pitch_deg = math.degrees(pitch)
    if(pitch_deg > 90):
        pitch_deg=pitch_deg-180
    if(pitch_deg < -90):
        pitch_deg=pitch_deg+180
    
    yaw_deg = math.degrees(yaw)
    if(yaw_deg > 90):
        yaw_deg=yaw_deg-180
    if(yaw_deg < -90):
        yaw_deg=yaw_deg+180   
    # 返回角度值
    return pitch_deg, yaw_deg
def plane_distance_to_origin(A, B, C, x0, y0, z0):
    # 计算平面常数 D
    D = A * x0 + B * y0 + C * z0
    dis =math.sqrt(A**2 + B**2 + C**2)
    if(dis)==0:
        dis=1       
    # 计算平面到原点的距离

    distance = abs(D) / dis
    return distance

实物照片：

效果展示

四、心得总结

利用 TMF8821 dTOF 传感器实现平面角度测量的学习心得