**这是本文档旧的修订版!**
PWM(脉冲宽度调制)原理、应用以及实现
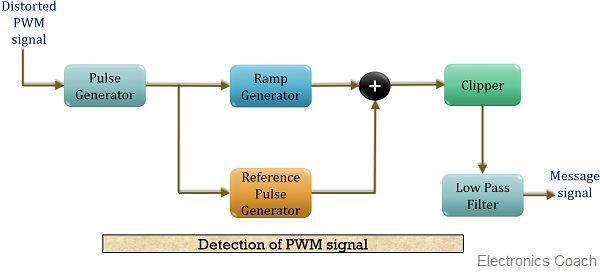
1. PWM的原理
PWM(Pulse Width Modulation)全称脉冲宽度调制,它通过对一系列脉冲的宽度进行调制,来等效地获得所需要波形(含形状和幅值)。
面积等效原理
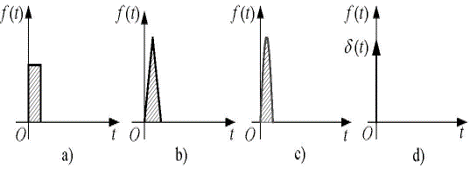
面积等效原理是PWM控制技术的重要理论基础。 原理内容:冲量相等而形状不同的窄脉冲加在具有惯性的环节上时,其效果基本相同。
- 冲量即指窄脉冲的面积。
- 效果基本相同,是指环节的输出响应波形基本相同。
- 如果把各输出波形用傅里叶变换分析,则其低频段非常接近,仅在高频 段略有差异。
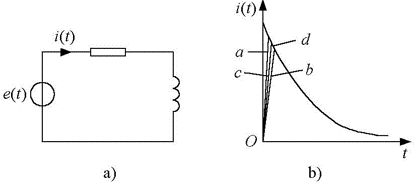
- 将图1a、b、c、d所示的脉冲作为输入,加在图2a所示的R-L电路 上,设其电流i(t)为电路的输出,图2b给出了不同窄脉冲时i(t)的响应波形。
| 图1:形状不同而冲量相同的各种窄脉冲 | 图2:冲量相同的各种窄脉冲的响应波形 | |
|---|---|---|
用PWM波代替正弦半波
将正弦半波看成是由N个彼此相连的脉冲宽度为π/N,但幅值顶部是曲线且大小按正弦规律变化的脉冲序列组成的。
把上述脉冲序列利用相同数量的等幅而不等宽的矩形脉冲代替,使矩形脉冲的中点和相应正弦波部分的中点重合,
且使矩形脉冲和相应的正弦波部 分面积(冲量)相等,这就是PWM波形。
对于正弦波的负半周,也可以用同样的方法得到PWM波形。
脉冲的宽度按正弦规律变化而和正弦波等效的PWM波形,也称SPWM(Sinusoidal PWM)波形。
基于等效面积原理,PWM波形还可以等效成其他所需要的波形,如等效所需要的非正弦交流波形等。
PWM波形可分为等幅PWM波和不等幅PWM波两种,由直流电源产生的PWM波通常是等幅PWM波。
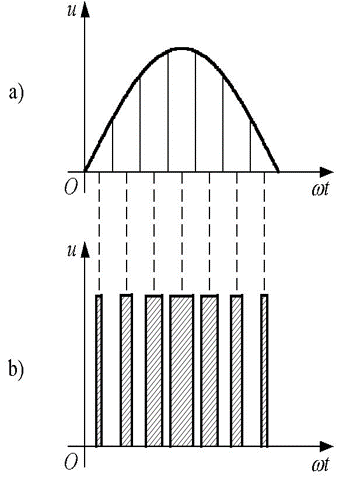
| 图3:用PWM波代替正弦半波 |
|---|
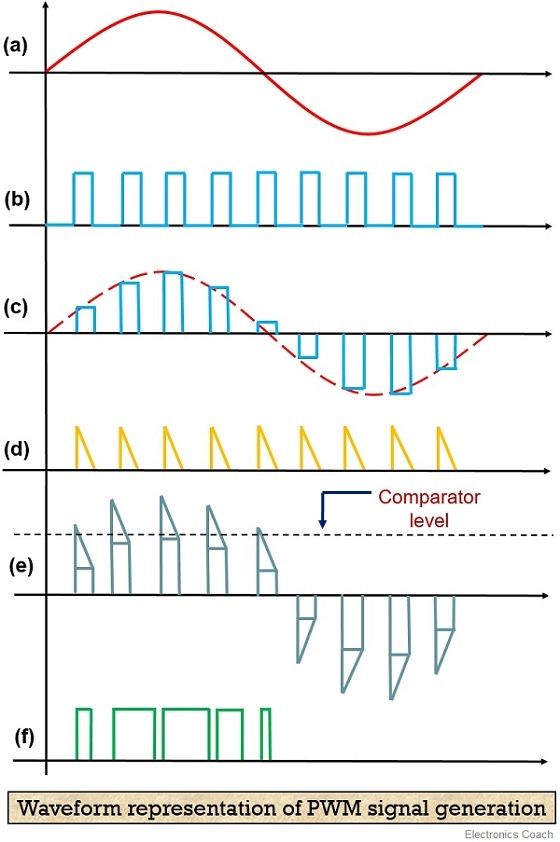
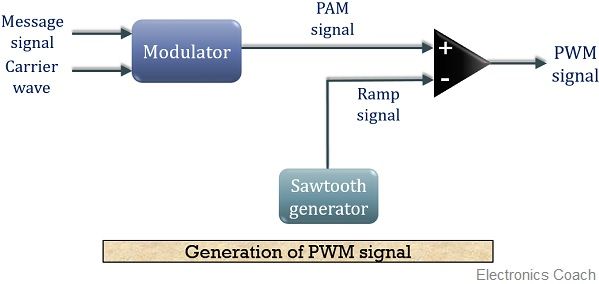
调制法生成PWM波形
把希望输出的波形作为调制信号,把接受调制的信号作为载波,通过信号波的调制得到所期望的PWM波形。
最简单可以产生一个脉冲宽度调制信号的方式是交集性方法(intersective method),
这个方法只需要使用锯齿波或三角波以及一个比较器。
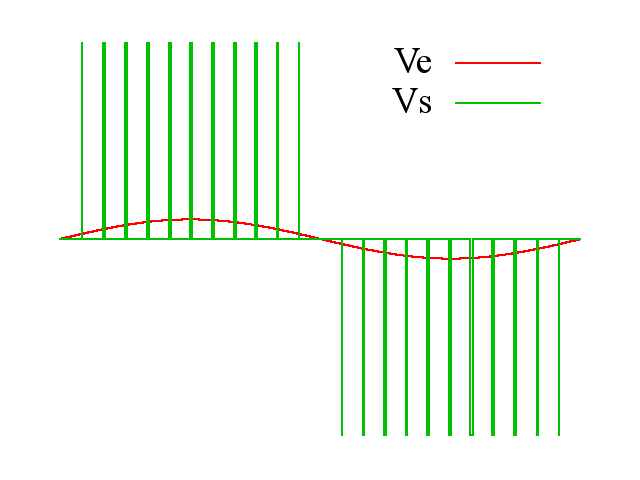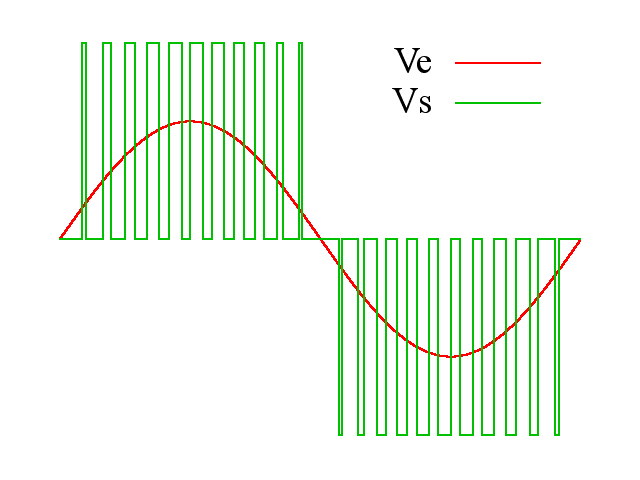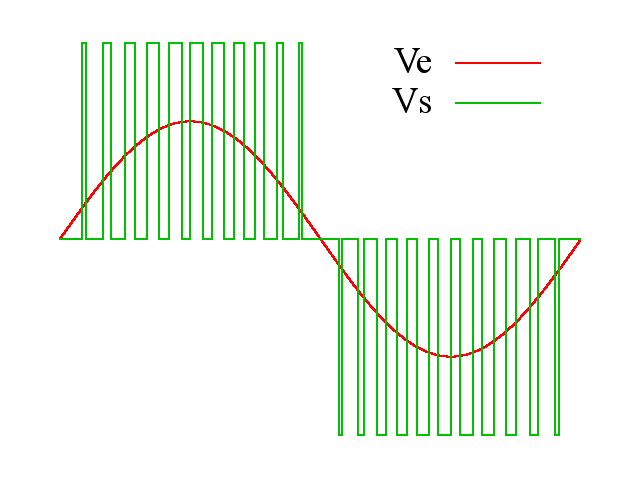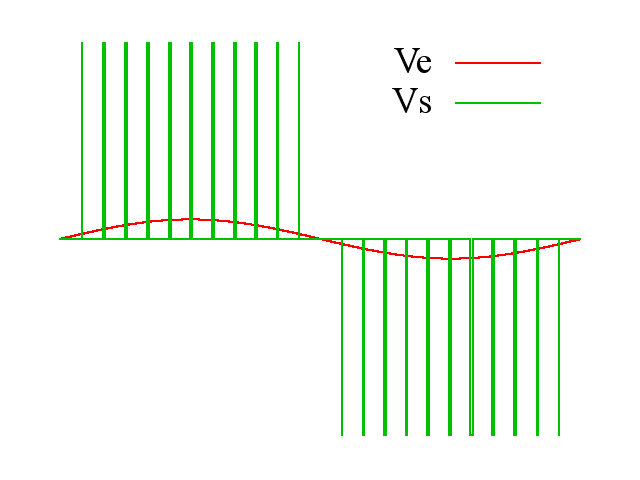
当参考的信号值(红色波)比锯齿波(蓝色波) 大,则脉冲调制后的结果会在高状态,反之,则在低状态。
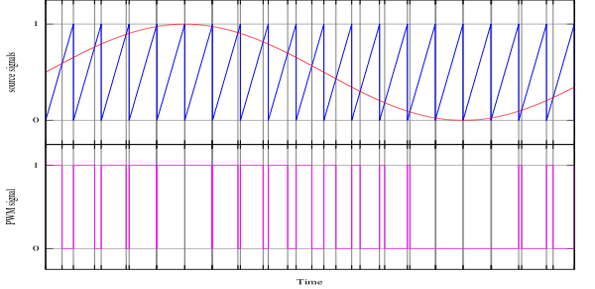
红色:调制信号;蓝色:载波信号;紫色:已调制信号
PWM信号参数
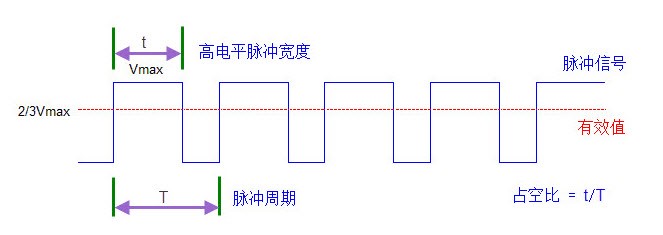
周期:信号变化的过程中,某段波形重复出现,其某一次开始至结束的这段时间就称为“周期“。
脉宽:在一个周期内正脉冲的持续时间。
占空比:是在一串理想的脉冲系列中,脉宽与周期的比值。例如在上图中t为正脉冲的持续时间,T为脉冲周期,占空比为t/T。
2. PWM的应用
- 使用PWM制作呼吸灯
- 使用PWM对LED调光
- 使用PWM制作电子琴
- 使用PWM驱动舵机
- 使用PWM驱动步进电机
- 使用PWM驱动直流减速电机
- 使用PWM实现DAC的功能
- 使用PWM实现直流稳压
3. PWM的实现方式
简而言之,PWM是一种对模拟信号电平进行数字编码的方法。通过高分辨率计数器的使用,方波的占空比被调制用来对一个具体模拟信号的电平进行编码。
PWM信号仍然是数字信号,而且幅值相等,在任意时刻,输出的信号就只有1(ON)或者0(OFF)两个状态,具体是0还是1,则由控制器来控制,也由控制器的精度决定。
只要带宽足够,任何模拟值都可以使用PWM进行编码。
既然PWM是数字信号,那么任何具有高低电平可控输出功能的数字芯片都可以生成PWM,比如最常用有微控制器(MCU),可编程逻辑FPGA,或是LED驱动控制芯片如PCA9685,以及各种电源用的控制芯片,以上都可以产生PWM波形,所以说PWM应用实在是太广了。
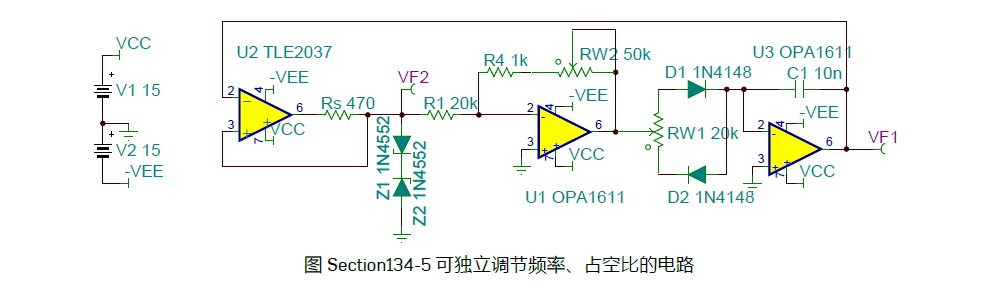
模拟器件搭建PWM电路
- 参考西安交大杨振国教授《新概念模拟电路V》
3.1 单片机(MCU)生成PWM
使用MCU生成PWM是最简单的方式,PWM发生功能和定时器功能是一起的,一种方法是使用软件设置定时器的定时时间,定时时间到翻转IO的高低电平,由于是软件来翻转电平,因此精度不能做到非常精确;另一种是直接使用定时器中的PWM功能,在定时器模块中已经集成了专用的PWM发生电路,用户只需要配置一下该模块的寄存器,在寄存器中配置好PWM的频率和占空比,软件使能该功能后,就可以输出精准的PWM波形。
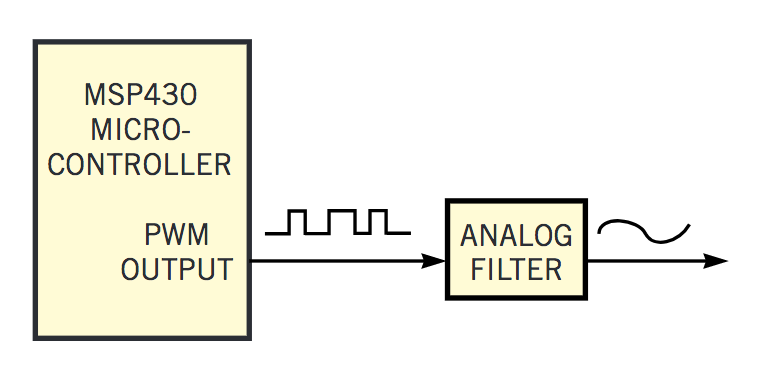
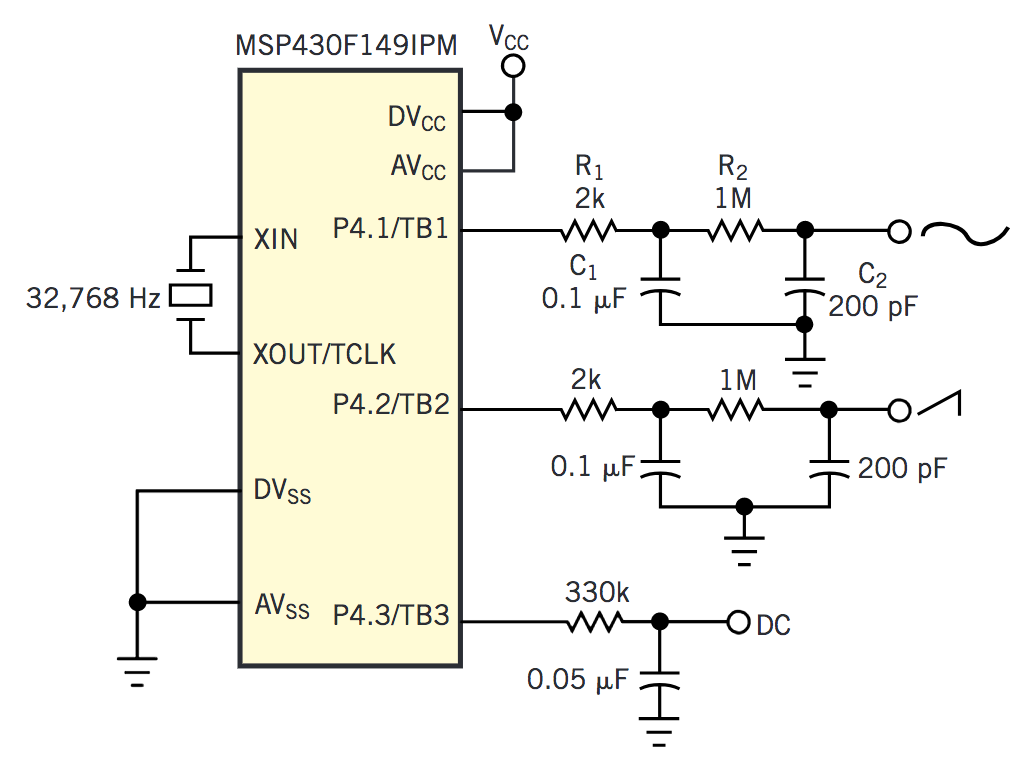
微控制器通过定时器输出PWM,再经过模拟低通滤波器得到模拟信号
每一路可以产生不同的信号
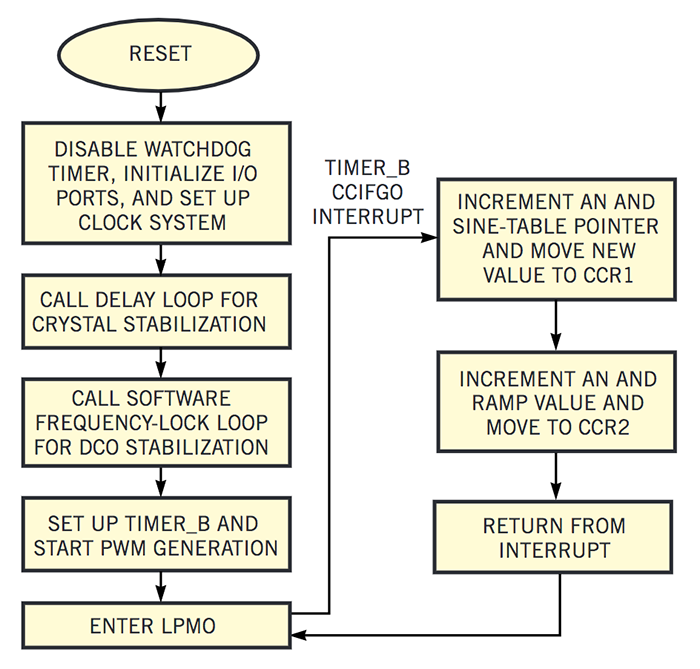
微控制器的软件流程
更多与微控制器定时器生成PWM信号的信息参见技术文章:使用微控制器的PWM定时器作为DAC
3.2 用Verilog生成PWM
参见文章:PWM的应用及相应的Verilog代码
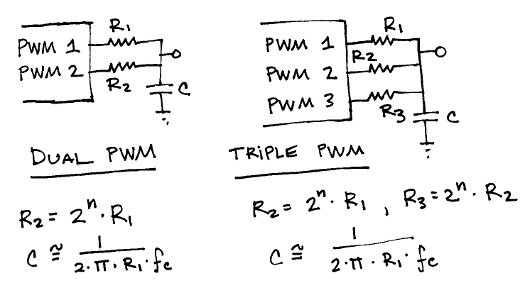
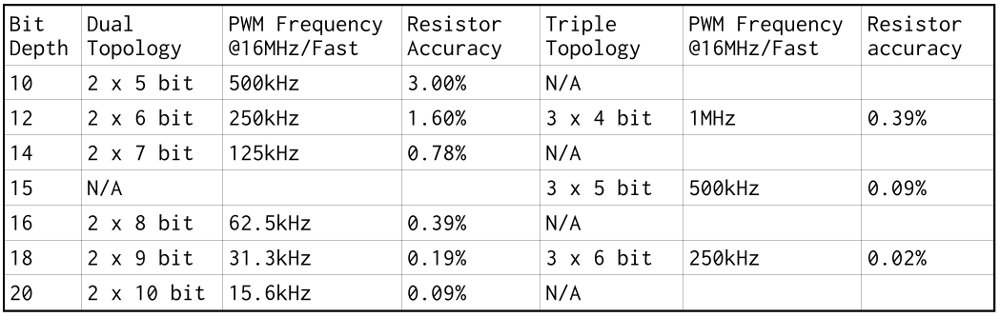
3.3 双PWM扩展转换频率和分辨率
采用多PWM输出扩展工作频率和分辨率的图示
为方便测试和验证,特用KiCad设计了一块测试板,电路原理图和PCB的3D效果图如下,图中的阻、容参数可以根据实际使用的位数以及转换频率、要生成的波形的频率进行调整。在此电路中的值为16位DAC设置。
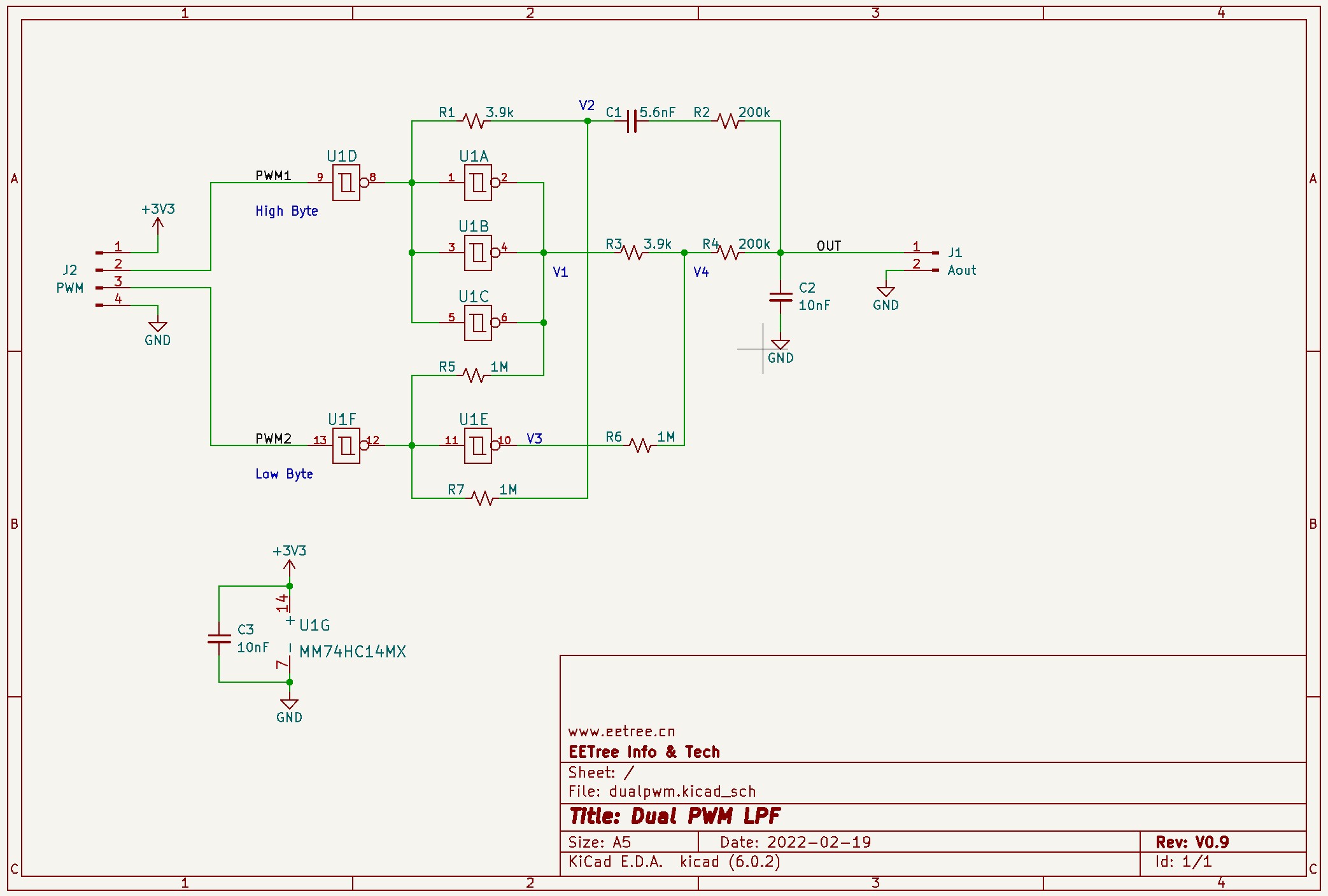
双PWM的原理图,用KiCad绘制
双PWM的PCB 3D,用KiCad绘制
import time, _thread, sys from machine import Pin, PWM import math import uarray pwmA = PWM(Pin(1, Pin.OUT)) # upper 4 bits pwmB = PWM(Pin(0, Pin.OUT)) # low 4 bits # Set the PWM frequency. pwmFreq= int(125_000_000/16) # 4 bit pwmA.freq(pwmFreq) pwmB.freq(pwmFreq) pwmA.duty_u16(31<<10) # upper pwmB.duty_u16(0<<10) sineBufLen= 500 #for 1kHz and 500kHz update frequ sineBuf=uarray.array("H",range(0,sineBufLen)) def setAmpl(amp): global sineBuf for x in range(0,sineBufLen): xr= x/sineBufLen*2*math.pi sineBuf[x]= 127 +int(amp*math.sin(xr)) # 8 bit resolution #print(sineBuf[x]) ddsCtrl = uarray.array('i',[ 0x40050000 + 0x0c, # 0 cc7, Counter compare values, Channel 7 sineBufLen, # 4 0x40054000 + 0x28, # 8 TIMERAWL Register 1 MHz S. 553, Raw read from bits 31:0 of time (no side effects) int((1<<16)*1.0) # 12 Index Step <>0 run, step in half words ]) @micropython.asm_thumb def dds(r0, r1): # Buffer, ctrl-array mov(r2,r0) # Buffer Start Address ldr(r5, [r1,4]) # buffer length ldr(r4, [r1,0]) # pwm counter compare register mov(r3,0) # Buffer Index fine label(nextVal) label(waitLoop) ldr(r6, [r1,8]) # Timer address ldr(r6, [r6,0]) # 1Mhz Timer lsr(r6,r6,1) # 500kHz cmp(r6,r7) beq(waitLoop) mov(r7,r6) # store time slice lsr(r0,r3,16) # index coarse lsl(r0,r0,1) # index coarse half words add(r0,r0,r2) ldrh(r0,[r0,0]) # read buffer regPoke(0x40050000 + 0x98, ((a>>6)<<16) + (a&63)) lsl(r6,r0,28) # get the lowest 4 bits lsr(r0,r0,4) # shift bits right (upper) lsl(r0,r0,16) lsr(r6,r6,28) # lower 4 bits add(r0,r0,r6) str(r0,[r4,0]) #b(retu) ldr(r6, [r1,12]) # reload step index repeat? cmp(r6,0) beq(retu) add(r3,r3,r6) # next buffer index fine lsr(r0,r3,16) cmp(r5,r0) # end not yet reached bhi(nextVal) lsl(r0,r5,16) sub(r3,r3,r0) mov(r0,r3) b(nextVal) label(retu) def setF(f): ddsCtrl[3]=int(f/1000*(1<<16)) def ddsWrap(sineBuf, ddsCtrl): dds(sineBuf, ddsCtrl) _thread.exit() _thread.start_new_thread(ddsWrap,(sineBuf, ddsCtrl)) setAmpl(127) setF(20000)
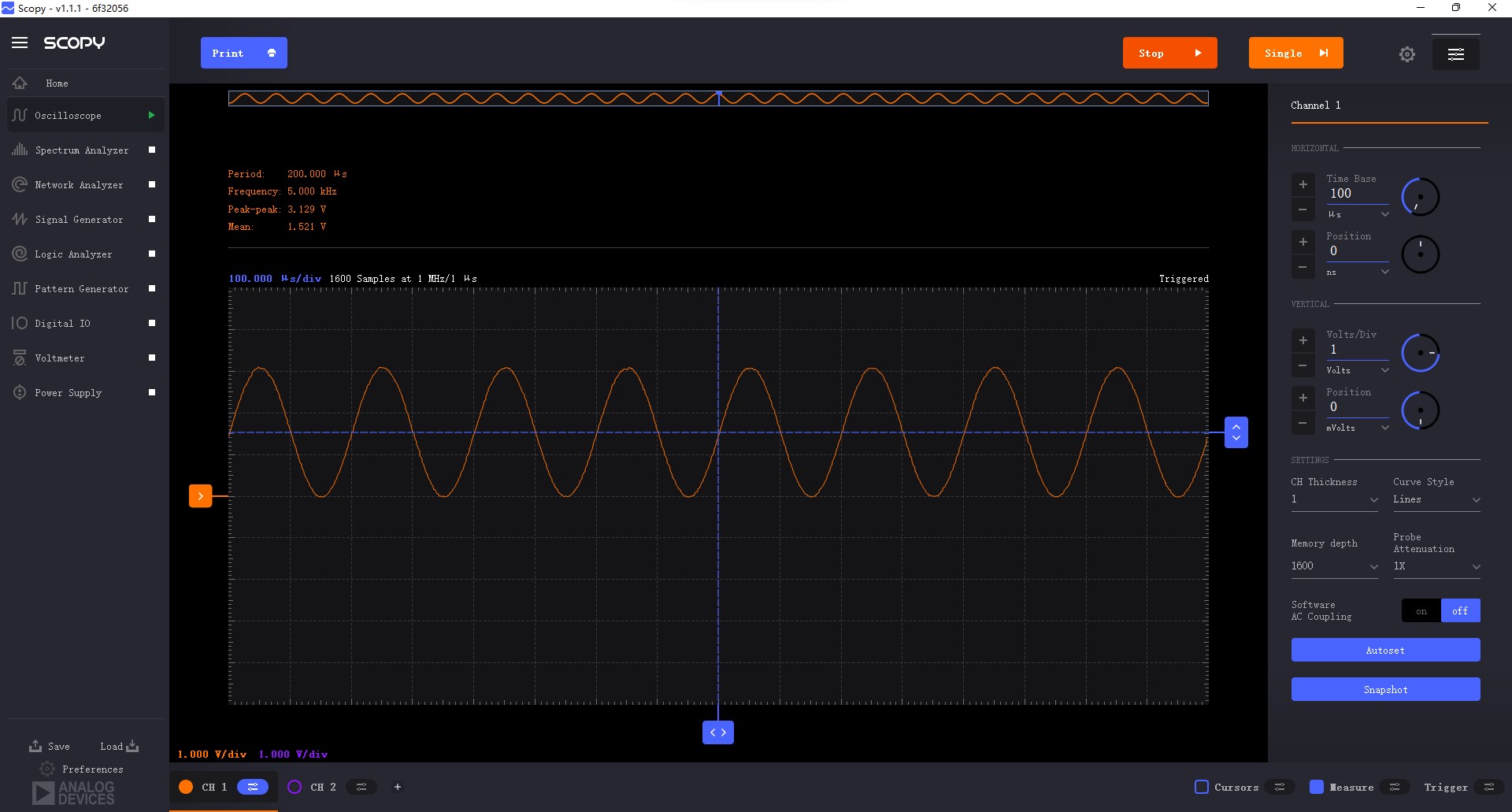
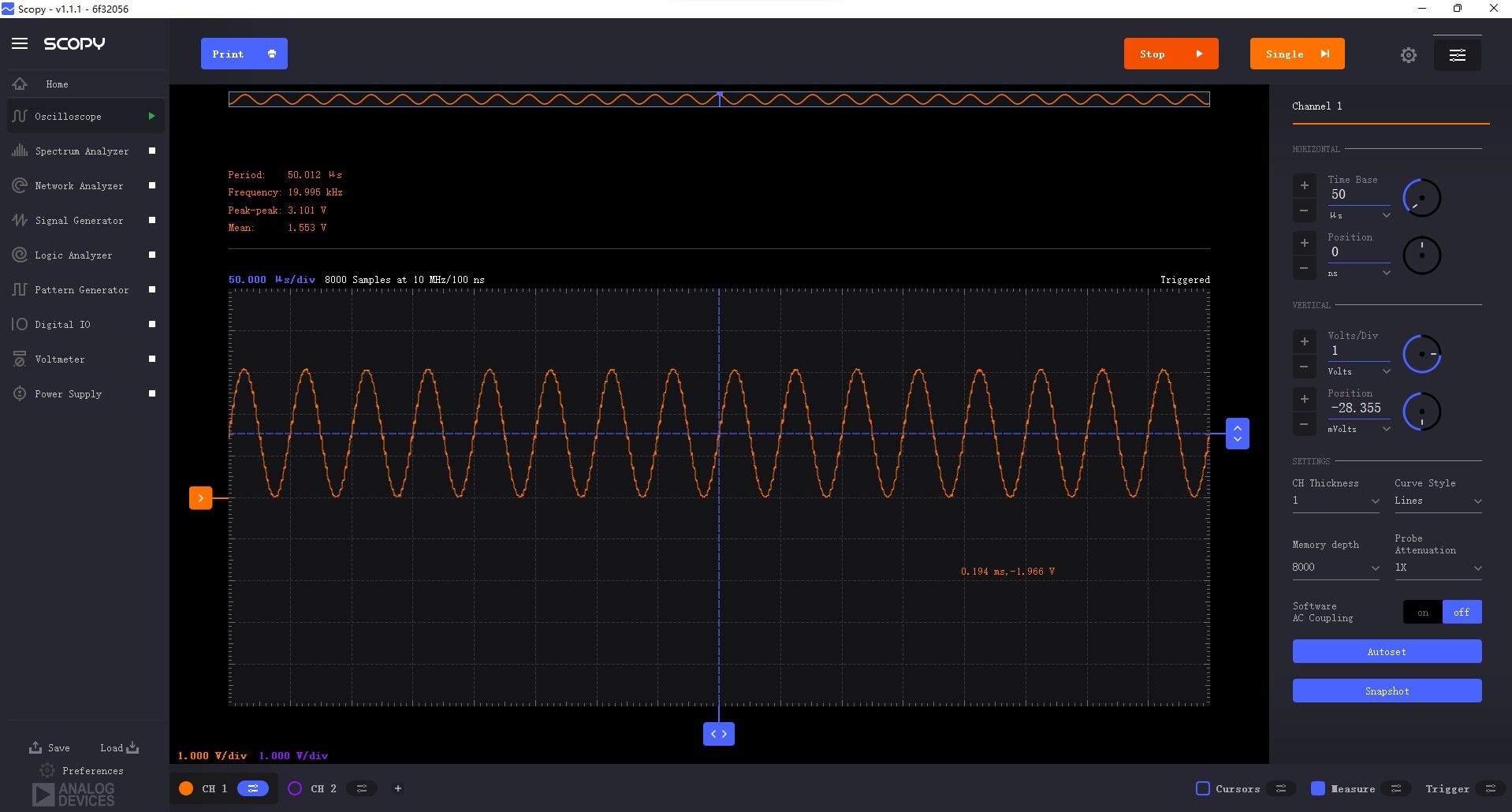
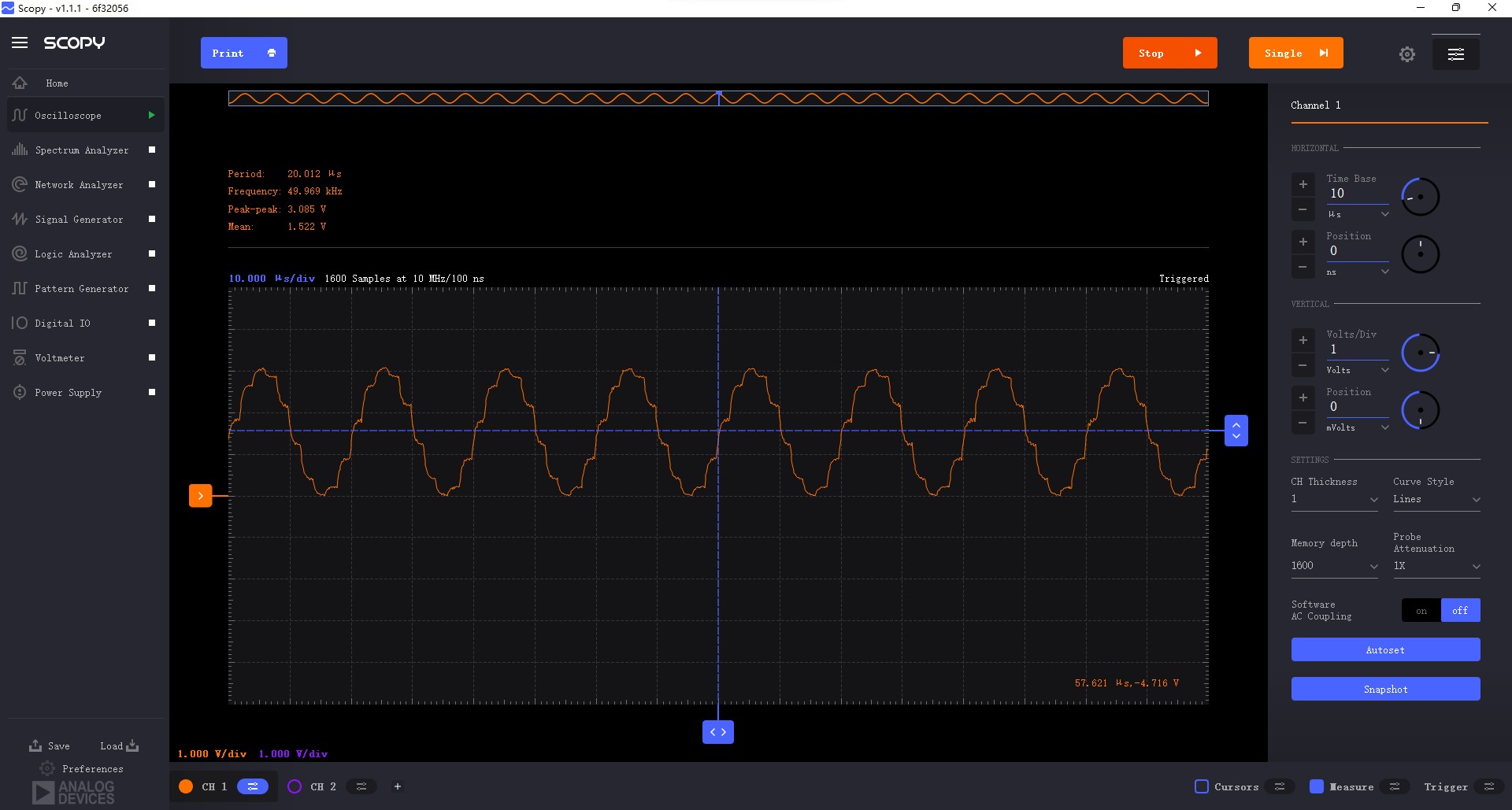
生成的5KHz的正弦波信号
生成的20KHz的正弦波信号
生成的50KHz的正弦波信号,低通滤波器截至频率太低
4. 示例
5. 参考文章
PWM(1)- 独臂神通
PWM可以算是数字电路中的“独臂”神通,“独臂” - 只需一根线;“神通” - 在很多关键的应用中起到栋梁的作用。PWM(脉宽调制 Pulse Width Modulation)从字面意思上讲它是一种“调制”方式,调制就意味着在某些载波信号上携带了某些的信息,通过解调的过程就可以得到其携带的信息,这些信息的属性由PWM的产生端定义,总之在这一根仅仅发生0、1交替变化的信号线上可以做出很多文章。
今天我们就看看如何通过PWM的方式实现数字到模拟变换的功能,也就是通过改变一根管脚的输出脉冲,得到模拟世界的某种波形。
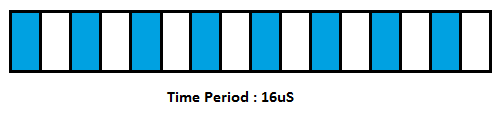
首先PWM是由一串连续行走在某输出管脚上的0、1交替出现的信号组成,我们称高电平1为ON,低电平0为OFF,ON+OFF为一个周期T,ON的持续时间除以周期T就为占空比 - Duty Cycle,看下面的两个图。
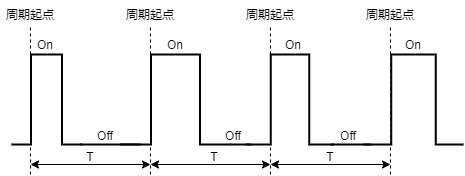
PWM波形, 高电平1为ON,低电平0为OFF, 占空比(Duty Cycle)为高电平持续时间除以周期
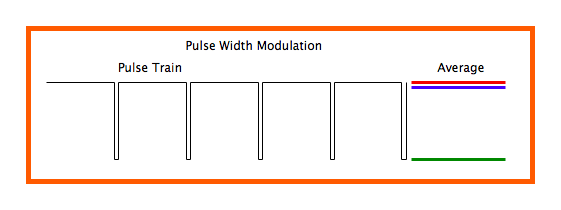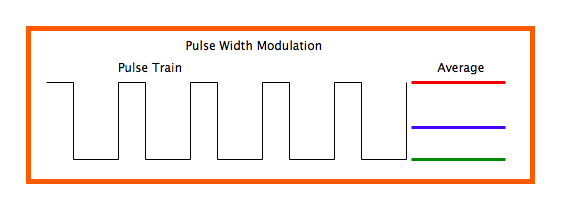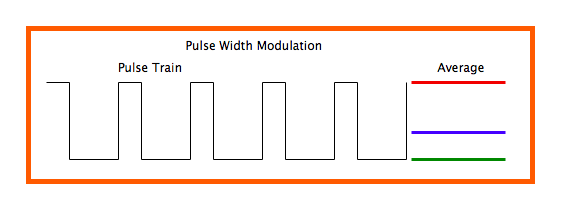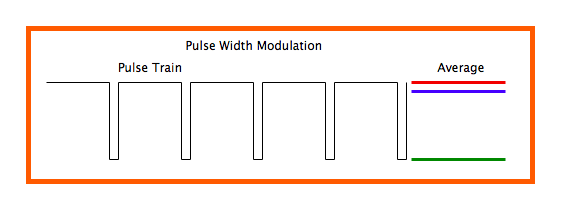
如果发送端用脉冲的占空比来传递“电压值”,也就是将某个数字的电压值对脉冲的占空比进行调制,就可以在接收端通过RC低通滤波器(也就是解调器)从调制脉宽的数据流中得到需要的模拟电压值,从而达到DAC的目的。看下面的动图 - 假设脉冲的占空比为0的时候(整个周期全部为OFF - 低电平)代表电压值为0,占空比为100%的时候(整个周期全部为ON - 高电平)代表电压值为最高电压,比如3.3V,则40%的占空比就是40%*3.3V。占空比改变-每个周期的脉宽改变,也就意味着输出的电压值在改变。
用脉宽的改变携带电压值的变化信息
用一个电阻和电容组成的低通滤波就可以将PWM中携带的电压信息“解调”成模拟的电压值
用一个电阻和电容组成的低通滤波就可以将PWM中携带的电压信息“解调”成模拟的电压值
用一个电阻和电容组成的低通滤波就可以将PWM中携带的电压信息“解调”成模拟的电压值
前面讲过DAC的两个关键指标 - 转换率和转换精度,在PWM里是如何对应的这两个指标么?
看一下下面的波形:
- PWM-DAC的转换频率相当于脉冲的重复频率
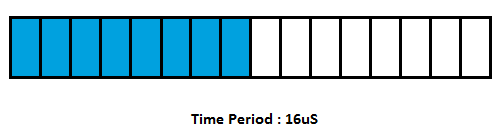
- PWM-DAC的分辨率相当于脉冲宽度相对于整个周期的精度,举例如果一个最小的脉冲ON的时间为5ns(可以用100MHz的时钟计数产生),PWM脉冲的周期为5ns x 256 = 1.28us,则这个PWM-DAC相当于是8位的DAC。
用时钟计数生成PWM波形,周期/占空比与主时钟的关系示意
也就是说如果你用100MHz的时钟来通过PWM的方式做一个8位的DAC,最高的转换频率也只能到1/1.28us ~ 781KHz分辨率高则转换率降低,因此用PWM做的DAC一般用于生成相对比较低频的信号乃至直流信号。
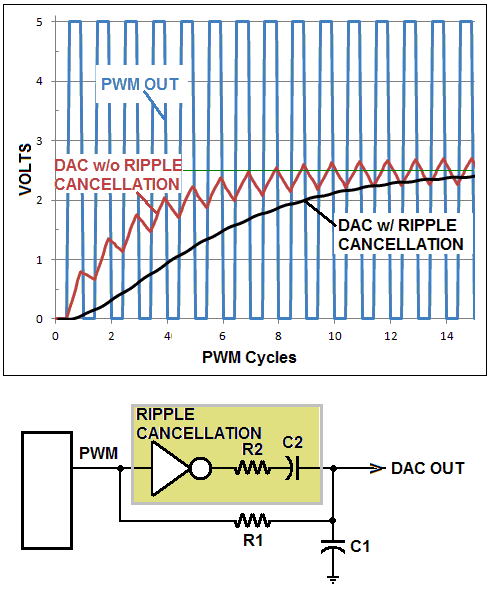
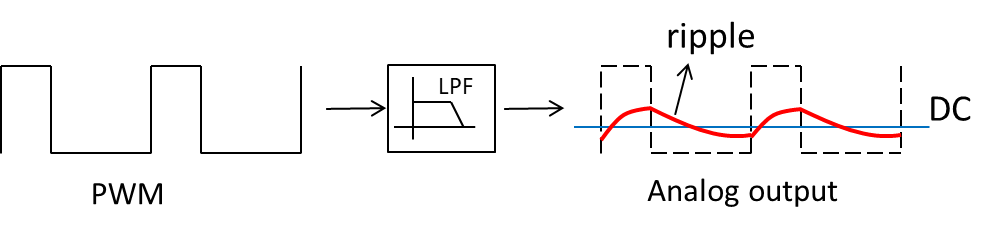
下面的图为经过一个最简单的由一个电阻R和一个电容C构成的低通滤波以后得到的模拟信号,可以看到在输出的模拟信号上还是有很高频率的纹波。
用一个电阻和电容组成的低通滤波就可以将PWM中携带的电压信息“解调”成模拟的电压值
如果要进一步平滑输出模拟信号上的波纹,可以通过加入电感或着用运算放大器构成的有源低通滤波器来对纹波实现更强的抑制。
是不是很简单?只需一个R和一个C就能得到你想生成的模拟信号,做一个简单的任意波形发生器很简单啊。
很多MCU都有内置的ADC,但未必有DAC,如果你选用的MCU/单片机没有内置的DAC,只需要一根管脚和俩器件(R、C)就能实现DAC的功能还是很有用的,即便拟选用的MCU内部有DAC,如果你的系统中需要多个DAC的功能,且你也不想或者没有足够的管脚外挂一个单独的DAC器件(需要I2C或SPI总线连接),PWM方式是个非常不错的选择哦。
如果你用的是FPGA或CPLD,里面根本没有DAC,而你又需要一个,拿出一个管脚来产生PWM就会非常666。
理解用PWM生成DAC的机制、局限,在关键的时候也许就能起到意料不到的结果。
PWM(2)- DAC的滤波器设计
昨天的文章写了如何通过PWM实现数字到模拟量的转换,得到很多朋友们的反馈,大家都比较感兴趣的如何选用电阻和电容的值才能得到一个满意的模拟值(低纹波)?
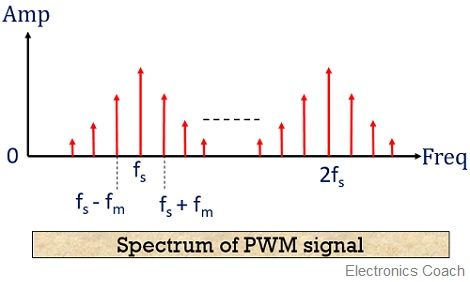
首先我们看一下脉冲信号的频谱,根据傅立叶变换,周期为T的脉冲信号可以分解为多个单频率的信号的叠加,最小的频率分量为1/T,有兴趣的同学可以通过Matlab自己做一下分析。
图片
比如,我们对幅度为3.3V、周期为10uS(频率100KHz)、占空比为50%的脉冲信号(此时为方波)进行FFT变换,可以得到1.65V的直流分量、100KHz、300KHz(3次谐波)、500KHz(5次谐波)。。。等频率分量,最小的交流频率为100KHz。
图片
占空比为50%的脉冲信号的波形
图片
占空比为50%的脉冲信号的频谱分量
改变占空比呢?来看看占空比为10%和90%的脉冲波形经过FFT之后的交流频率分量
图片
占空比为10%的脉冲的频率分量
图片
占空比为90%的脉冲的频率分量,只是直流分量不同,交流部分与10%的相同
从以上简单的分析可以看出,无论占空比是多少,脉冲波形除了直流分量以外,交流部分的最低频率都为脉冲的重复频率100KHz上,在DC和脉冲重复频率100KHz之间一马平川,光秃秃的。
因此,如果要得到直流分量,只需要去掉100KHz以上的频谱能量就可以了。最简单的方法就是通过由一个电阻R和一个电容C构成的一阶低通滤波器,其截止频率为fc=1/2PiR*C,我们要得到的是直流分量,滤除的是100KHz以上的频率,因此只要截止频率在100KHz以内,并且能对100KHz以上的所有频谱都有较好的抑制,就能够得到比较好的DC输出。
图片
LPF电路构成和频率响应
图片
RC电路的时域响应
可以想象,截止频率越高,越是接近要滤除的频率(比如50KHz之于100KHz),该滤波器对100KHz的滤波效果就较差,就会有一定量的残余能量出现在滤波器的输出端,如下图,也就是输出的波形纹波比较高。
图片
对脉冲频率为100KHz的信号进行截止频率为50KHz的低通滤波得到的输出信号,纹波比较高
如果降低截止频率,越是接近直流,从而距离要滤除的频率越远,比如针对100KHz的脉冲频率选择1KHz作为LPF的截止频率,则在100KHz处可以达到非常高的抑制度,100KHz的残留就非常小,也就是在输出的直流信号上的纹波可以变得很小,见下图。
图片
截止频率为1KHz的低通滤波器的建立时间很长 ~ 1ms
但却出现了另外一个问题 - 需要花费很久的时间(学名叫建立时间 setting time)才能达到应该达到的DAC的直流值。原因就是fc低,意味着RC更高,也就是充电的时间常数变得很长 - R增大意味着对C进行充电的电流变小,要对C冲电到一定的值花费的时间也就更久。,
因此这就出现了一个让人纠结的选择: 选择较低的截止频率 - 较低的纹波,较长的建立时间 选择较高的截止频率 - 较大的纹波,较快的建立时间 你会说一阶不够,要不多用几阶滤波器,加上电感或者有源的运放来进行低通滤波,这确实能改善滤波的效果,但 – 电路的复杂度增加、元器件成本增加了,且改善有限。
那不增加电路的复杂程度,还是只用这一个R和一个C是否能够改善性能呢? 答案是肯定的,其实也很简单 - 把交流分量的频率踢的远远的,在保持较低的时间常数(建立时间短)的情况下,将LPF的截止频率fc和要滤除的脉冲重复频率之间的间隔尽可能的拉开,比如将100KHz的重复频率给踢到10MHz(出去100倍),占空比不变,如果用原来的50KHz的滤波器,到了10MHz的地方怎么也把10MHz以上的频率给消灭的只剩下一点渣了。看下图,直流建立时间大约为15µs, 纹波变得只有25mV左右了。
图片 用截止频率为50KHz的RC得到的建立时间大约为15µs
图片 用截止频率为50KHz的RC对10MHz的脉冲信号进行LPF得到的纹波
是不是很神奇?其实理论依据很简单,自己把低通滤波器的频响曲线画一下就很容易理解了。 到这里我们就应该知道如何设计自己的PWM系统的各项参数来构造一个简单好用的DAC。