目录
使用Verilog来编程FPGA
1. 逻辑
FPGA是依赖数字逻辑的数字器件,计算机硬件使用的是数字逻辑,每一个计算,屏幕上每一个像素的呈现,音乐轨的每一个note都是使用数字逻辑构成的功能块来实现的。 虽然多数时候,数字逻辑是抽象的数学概念,而不是物理电子,逻辑门以及其它的数字逻辑器件则是由刻蚀在集成电路上的晶体管来实现的。对于FPGA来讲,可以通过绘制逻辑门构成的电路,将这些门映射到FPGA的通用门上,并将它们连接起来以实现你设想的逻辑设计。 另外一种方式是,使用Verilog(或其它的)硬件描述语言来实现逻辑。 你依然可以购买能够实现小数量逻辑门的器件,比如7400,内部只有4个二输入与非门,然而这些器件只是为了维护一些古老的系统或用于教学。
逻辑门
逻辑门有输入和输出,这些数字输入和输出可以是“高”或者“低”, 无论是输入端还是输出端,所谓的“低”指的是接近于0V(地)的电压,而“高”一般是超过提供给该逻辑器件的供电电压一半以上的电压,给FPGA提供的电压一般为1.8V、3.3V或着5V中的一个,多数的FPGA的工作电压范围有一定的冗余度,有些FPGA允许在一个器件中存在多个逻辑电压.
与非门和或非门都是非常通用的门,因为只需要反相它们的输入端或输出端就可以构成其它任何一种门,另外你可以用与非门或着或非门构成非门,只需要将两个输入信号连接在一起就可以。例如图1.6中你可以用3个或非门构成一个与门。
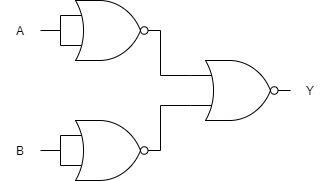
图1.6 用3个“或非门”构成一个“与门”
De Morgan定律
图1.6的设计利用了逻辑定律中的De Morgan定律 - 将两个输入端“与”后的结果进行取反,和先将两个输入端进行取反以后再“或”得到的结果是一样的。在图1.6中,两个输入端信号先被由“或非门”构成的“非门”取反以后进行“或”操作,再对输出的结果取反。
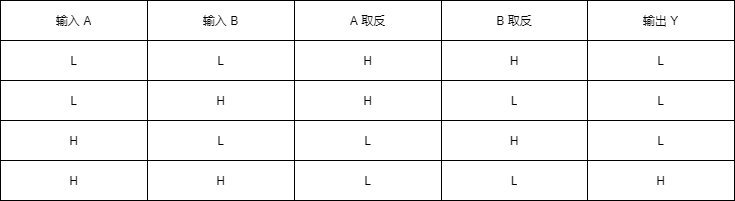
表1.6 用多个异或门构成一个与门的真值表
二进制
我们前面将逻辑门的输入和输出端以电压的高低来表示,我们还可以将它们用数字来表示 - 1表示高电平,0表示低电平,这样我们就可以想明白计算机是如何使用逻辑门来操作数字的了。当然,我们仅有数值0和1是不够用的。
在我们的生活中都是使用10进制,主要的原因是因为我们有10根手指,如果我们的老祖宗使用鼻子来计数,那就是二进制了,因为结果只有0还是1,如果要表示多于1个的数字,你可以用多个二进制数值(bit - binary digit)来表示。
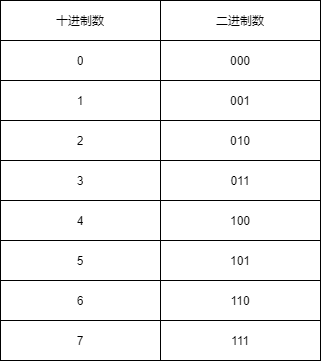
表1.8 用二进制和十进制表示的数字0到7
用逻辑实现的“加法”
你可以用逻辑门来对二进制数进行运算,因为二进制数只是用“位”(bit)表示的数值,你可以用逻辑针对任何数值进行运算。图1.8展示了如何用逻辑门进行一个二进制加。

图1.8 一个1位加法器
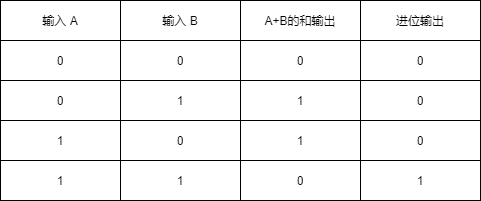
表1.9 一个1位加法器的真值表
从表中可以看出,如果输入端A和B都是0,加法的结果位0, 如果其中一个输入为1,加法的结果为1,然后如果两个输入端都为1,加法的位本身就变成了0,但我们希望将进位输出的1放到下一位,在二进制中,1+1位0,并一个进位(或十进制的2)
这就意味着,如果我们同时加多于一位的数值,下一个加法的部分将有3个输入(A、B和进位输入),这就需要三个位的加法,图1.9展示了计入进位以后的加法。

图1.9 一个带有进位输入端的1位加法器
你也许永远不会用这种方式通过多个门来构建一个加法器,因为有现成的加法器芯片可以用于你的设计,在这里你能够看到加法器是如何通过门电路构成的。 如果我们有8级这样的电路,就可以实现2个字节的加法操作,每一个计算机的中央处理器(CPU)都有这种用逻辑门搭建的硬件加法器,一个32位的处理器可以同时处理32位的数值,一个64位的机器能够通过64个图1.9的方式同时将64位数字加起来。
触发器 - Set-Reset触发器
移位寄存器
二进制计数器
总结
2. FPGA
FPGA是如何工作的?
小脚丫FPGA板
软件设置 - 安装Diamond/Quartus
项目文件
总结
3. 图形化设计逻辑
一个数据选择示例
- 第一步:创建一个项目
- 第二步:创建一个新的原理图
- 第三步:添加一个逻辑符号
- 第四步:连接各个门
- 第五步:添加输入输出(IO)标记
- 第六步:创建一个用户约束文件
- 第七步:生成.bit文件
- 第八步:编程你的板子
- 测试结果
一个4位计数器示例
- 绘制原理图
- 实现约束文件
- 测试计数器
总结
介绍Verilog
模块
Wires,Registers,Buses
并行执行
数值的格式
使用Verilog来实现数据选择
使用Verilog来实现计数器
同步逻辑
总结
4. 模块化Verilog
一个7段译码器
按键消抖
复用的7段数码管和计数器
- 项目结构
- Display7seg
- Counter_7_seg
- 用户约束文件
- 向模块导入源代码
- 设置顶层模块
- 3-digit版本
- 测试
总结
5. 定时举例
状态机
状态机设计
硬件
- 你需要 —
- 结构
模块
用户约束文件
定时模块
- 输入和输出
- 按键
- 报警模块Instance
- 为时间和显示建模
- 状态机实现
测试
总结
6. PWM和伺服电机
脉宽调制
一个PWM模块
- PWM模块的输入和输出
- PWM模块的测试程序
- 试一下
伺服电机
硬件
- 你需要的 —
- 构建
一个伺服模块
总结
7. 音频处理
简单的音调发生器
从小脚丫FPGA上声音输出
- 一个通用的音调/频率发生器
- 音调模块
- tone_tester模块
- 测试
播放一个音频文件
- 音频文件
- RAM
- wav_player模块
- 测试
- 准备好你的声音
总结
8. 视频处理
VGA
VGA的时序
画一个长方形
- 一个VGA模块
- VGA和小脚丫FPGA
移动物体
一个存储器映射的显示
- 准备一个图片