2024艾迈斯欧司朗竞赛 - 基于TMF8821 dToF传感器模块和STM32G431实现的角度测算

内容介绍

一.项目介绍

本项目基于TMF8821 dToF传感器模块和STM32G431单片机实现角度测算功能，要求如下：

将板卡组合后固定,并保证与面前的平面存在一定夹角，通过程序测算出板卡距离平面的夹角和垂直最小距离。

二．硬件介绍

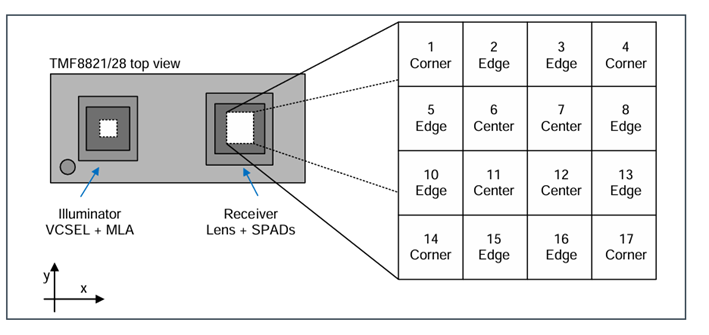
TMF8821是一款直接飞行时间（dToF）传感器，采用单一模组封装，配有VCSEL。这款dToF器件采用SPAD、TDC和直方图技术，实现了5000 mm的检测范围。SPAD上装配有透镜，可支持3×3、4×4和3×6多区输出数据和动态可调的视场角。封装内部配有多透镜阵列（MLA），位于VCSEL上方，可拓宽FoI（发射角）。所有原始数据的处理都在片上进行，TMF8821通过其I2C接口提供距离信息以及置信度值。

STM32G431基于高性能Arm^® Cortex^®-M4 32位RISC内核，带有单精度浮点运算单元 (FPU)，支持所有Arm单精度数据处理指令和所有数据类型，I²C支持增强快速模式 (1 Mbps)。

三.设计思路

设备驱动上，官方提供了基于Arduino的c语言例程，基于该例程修改了抽象层（shim.c/.h）来适配STM32 HAL库实现简单驱动。

通过更改SPAD掩码使用4x4区域测量

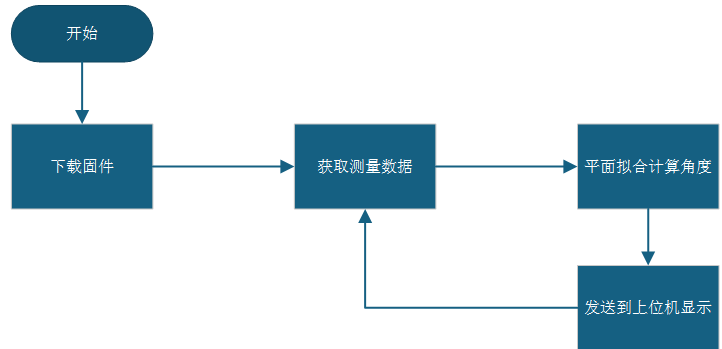
经过查询资料，发现可以使用最小二乘法拟合平面实现角度测算和距离测量，流程如下

坐标系转换：

将距离数据转换到笛卡尔坐标系

使用球坐标变换公式，考虑传感器的视场角

平面拟合：

使用最小二乘法拟合平面方程 z = ax + by + c

通过解线性方程组得到平面参数

角度计算：

用平面法向量计算俯仰角（pitch）和横滚角（roll）

使用atan2函数确保角度方向的正确性

距离计算：

计算传感器到平面的垂直距离

使用平面方程常数项进行归一化计算

获取结果后即可通过串口发送到上位机。

四．软件流程及关键代码

4.1 部分抽象层代码，实现i2c，延时，GPIO,串口打印等功能

// I2C写寄存器
int8_t i2cTxReg(void *dptr, uint8_t slaveAddr, uint8_t regAddr, uint16_t toTx, const uint8_t *txData) {
    HAL_StatusTypeDef status = HAL_I2C_Mem_Write(TMF8828_I2C_HANDLE, slaveAddr << 1, regAddr, I2C_MEMADD_SIZE_8BIT, (uint8_t *)txData, toTx, HAL_MAX_DELAY);
    return (status == HAL_OK) ? I2C_SUCCESS : I2C_ERR_TIMEOUT;
}

// I2C读寄存器
int8_t i2cRxReg(void *dptr, uint8_t slaveAddr, uint8_t regAddr, uint16_t toRx, uint8_t *rxData) {
    HAL_StatusTypeDef status = HAL_I2C_Mem_Read(TMF8828_I2C_HANDLE, slaveAddr << 1, regAddr, I2C_MEMADD_SIZE_8BIT, rxData, toRx, HAL_MAX_DELAY);
    return (status == HAL_OK) ? I2C_SUCCESS : I2C_ERR_TIMEOUT;
}

// 替换enablePinHigh函数
void enablePinHigh(tmf8828Driver *driver)
{
HAL_GPIO_WritePin(ENABLE_GPIO_PORT, ENABLE_PIN, GPIO_PIN_SET);
}

// 替换enablePinLow函数
void enablePinLow(tmf8828Driver *driver)
{
HAL_GPIO_WritePin(ENABLE_GPIO_PORT, ENABLE_PIN, GPIO_PIN_RESET);
}

4.2 最小二乘法拟合平面实现角度测算和距离测量

// 将角度转换为弧度
double deg2rad(double deg) {
    return deg * PI / 180.0;
}
// 计算平面角度和距离
void calculate_plane(float distances[4][4], float *pitch, float *roll, float *distance) {
    float x[16], y[16], z[16];
    int idx = 0;

    // 将距离数据转换为三维坐标
    for (int i = 0; i < 4; i++) {
        for (int j = 0; j < 4; j++) {
            float dist = distances[i][j];
            // 计算水平和垂直角度
            float theta = deg2rad((j - 1.5) * PIXEL_FOV_X); // 水平方位角
            float phi = deg2rad((1.5-i) * PIXEL_FOV_Y);    // 垂直俯仰角

            // 转换为笛卡尔坐标系
            x[idx] = dist * sin(theta) * cos(phi);
            y[idx] = dist * sin(phi);
            z[idx] = dist * cos(theta) * cos(phi);
            idx++;
        }
    }

    // 构建最小二乘方程组
    float sum_x = 0, sum_y = 0, sum_z = 0;
    float sum_x2 = 0, sum_xy = 0, sum_xz = 0;
    float sum_y2 = 0, sum_yz = 0;

    for (int k = 0; k < 16; k++) {
        sum_x += x[k];
        sum_y += y[k];
        sum_z += z[k];
        sum_x2 += x[k] * x[k];
        sum_xy += x[k] * y[k];
        sum_xz += x[k] * z[k];
        sum_y2 += y[k] * y[k];
        sum_yz += y[k] * z[k];
    }

    // 构造矩阵方程 [a, b, c]
    float matrix[3][3] = {
        {sum_x2, sum_xy, sum_x},
        {sum_xy, sum_y2, sum_y},
        {sum_x, sum_y, 16}
    };
    float vector[3] = {sum_xz, sum_yz, sum_z};

    // 解线性方程组（使用克莱姆法则）
    float det = matrix[0][0] * (matrix[1][1]*matrix[2][2] - matrix[1][2]*matrix[2][1])
              - matrix[0][1] * (matrix[1][0]*matrix[2][2] - matrix[1][2]*matrix[2][0])
              + matrix[0][2] * (matrix[1][0]*matrix[2][1] - matrix[1][1]*matrix[2][0]);

    if (fabs(det) < 1e-6) {
        *pitch = *roll = *distance = 0;
        return;
    }

    float a = (vector[0] * (matrix[1][1]*matrix[2][2] - matrix[1][2]*matrix[2][1]) -
              matrix[0][1] * (vector[1]*matrix[2][2] - matrix[1][2]*vector[2]) +
              matrix[0][2] * (vector[1]*matrix[2][1] - matrix[1][1]*vector[2])) / det;

    float b = (matrix[0][0] * (vector[1]*matrix[2][2] - matrix[1][2]*vector[2]) -
              vector[0] * (matrix[1][0]*matrix[2][2] - matrix[1][2]*matrix[2][0]) +
              matrix[0][2] * (matrix[1][0]*vector[2] - vector[1]*matrix[2][0]) )/ det;

    float c = (matrix[0][0] * (matrix[1][1]*vector[2] - vector[1]*matrix[2][1]) -
              matrix[0][1] * (matrix[1][0]*vector[2] - vector[1]*matrix[2][0]) +
              vector[0] * (matrix[1][0]*matrix[2][1] - matrix[1][1]*matrix[2][0]) )/ det;

    // 计算平面参数
    float norm = sqrt(a*a + b*b + 1);
    float nx = a / norm;
    float ny = b / norm;
    float nz = 1.0 / norm;

    // 计算角度（单位：度）
    *pitch = atan2(ny, nz) * 180.0 / PI; // 俯仰角
    *roll = atan2(nx, nz) * 180.0 / PI;   // 横滚角
    *distance = fabs(c) / sqrt(a*a + b*b + 1); // 垂直距离
}

五．功能展示

可以测量出俯仰角，横滚角和垂直距离

六.遇到的问题

调试时对于3x3，4x4模式的调节和输出的数据格式产生了一些问题，阅读官方文档后可以解决。

七.感想与体会

本项目是我第一次从零开始上手使用一款模块，还是比较有挑战性。积累了光学传感器和多文件编程的经验。未来期望再次参加活动，了解并学习更多的知识，掌握更多的技能，开拓电子芯片在生活中运用的视野。