项目介绍

本项目是基于TMF8821的dToF传感器模块，搭配RP2040游戏机完成平面角度测量功能。

硬件介绍

RP2040

基于树莓派RP2040的嵌入式系统学习平台，可以通过C/C++以及MicroPython编程来学习嵌入式系统的工作原理和应用。

基于TMF8821的dToF传感器模块

TMF8821 dToF传感器模块是基于TMF8821传感器设计的一款dToF（direct Time-of-Flight，直接飞行时间）传感器，与RP2040游戏机管脚匹配，插上直接可以使用，模块侧面预留了扩展接口，可以自由焊接/调试/抓取数据。

数据手册和通讯手册如链接所示，接下来将对TMF8821模块做一个简要的原理讲解。

TMF8821功能简介

TMF8821 是一款集成VCSELL（Vertical-Cavity Surface-Emitting Laser，垂直腔面发射激光器）的直接飞行时间传感器，基于SPAD（Single Photon Avalanche Diode，单光子雪崩二极管）、TDC（Time-to-Digital Converter，时间数字转换器）和直方图技术，检测范围可达5000毫米。其透镜设计支持多种多区域输出数据（如3x3、4x4、3x6），并具有动态可调的宽视场。VCSE上方的MLA（Micro Lens Array，微透镜阵列）扩大了照明区域。所有数据处理均在芯片上完成，设备通过I²C接口输出距离信息和置信度值。

该设备适用于多种应用，包括手机相机的LDAF（Laser Detect Autofocus，激光检测自动对焦）、计算和通信中的存在检测、机器人技术中的物体检测与避障，以及工业领域的光幕应用。

该设备具有高信噪比、宽动态范围和无多径反射的优势，能够在黑暗和阳光环境下实现±5%精度的距离测量。其可调视场适应多种场景，提供最佳分辨率测距模式和高精度测量。设备支持动态盖板玻璃校准、污渍去除和串扰补偿，并具备眼安全保护功能。光学滤光片和算法增强了环境光抗干扰能力，同时其紧凑设计减少了电路板空间需求，适合低剖面系统设计和工业应用。

TMF8821工作原理分析

下图是TMF8821的模块框图，可以看到TMF8821通过I²C接口与主机进行通讯，并搭配了两个GPIO作为做扩展，可以用于编程配置。

TMF8821的工作原理是通过Driver模块驱动VCSEL脉冲序列照亮目标区域，发出的光被物体反射，反射光被Optical Filter滤光接收并投射到SPAD阵列上。TDC测量脉冲的发射和接收时间差，并将数据累积成直方图。内部的ARM处理器运行算法处理这些直方图数据，计算目标距离，最终从Control模块通过I²C接口输出每个区域的毫米级距离值。

前文提到，TMF8821支持多区域输出数据，下图是光学器件在XZ平面上的简要物理结构示意图。

可以看到在传感器基板（Sensor DIE）上分布了许多个SPAD用于测量光信号。XY方向上，SPAD分布情况和不同SPAD掩码对应的FOV情况如下图所示：

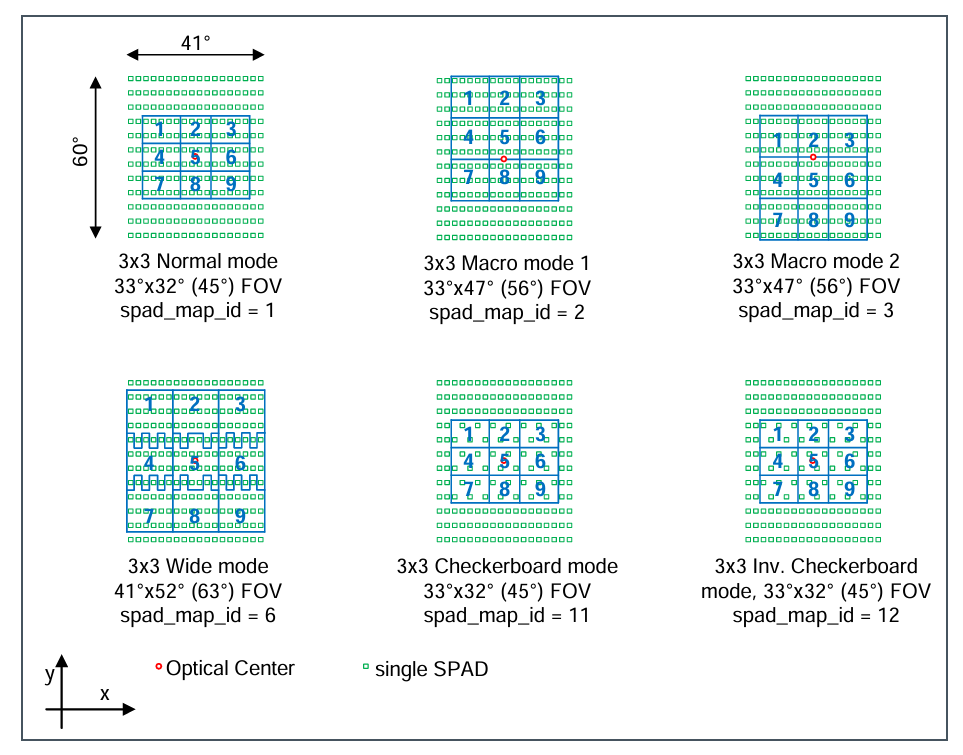
通过选择不同的spad_map_id可以调整至不同的测量模式，通过该图可以大致的计算出测量范围。测量结束后，可以通过读取寄存器0x24-0xa3来获取测量值和其他数值。

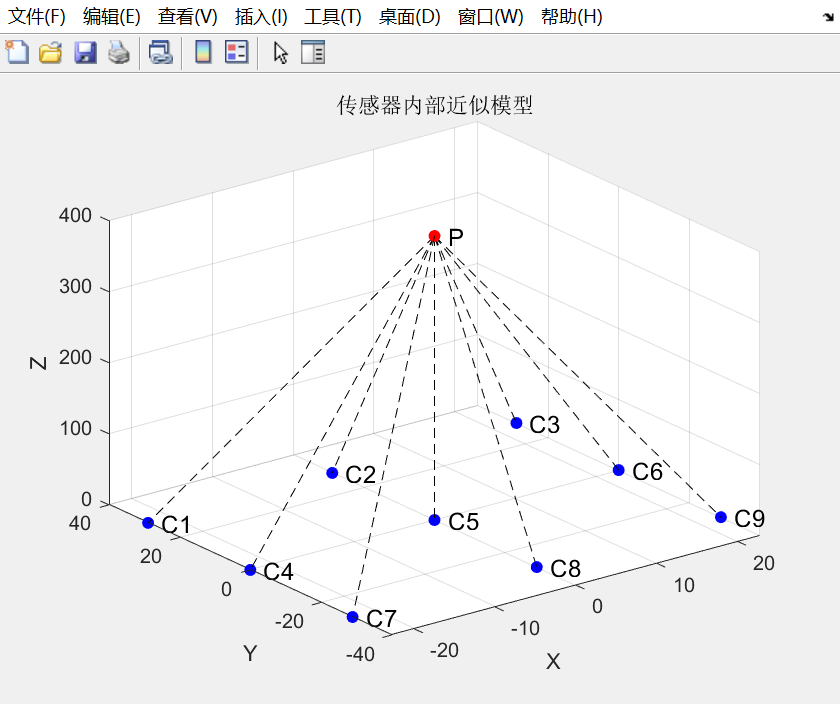
以通讯手册中的示例配置为例，选择spad_map_id=6，可以近似为下图，图中点P为透镜的光学中心，距离SPAD焦平面的距离是400微米，D1~D9为每个zone近似的中心点，由此可以计算出每个中心点到透镜光学中心的法向量$F_i$。

软件流程介绍

流程图如下：

RP2040的初始化由于在先前的活动中有很多项目均介绍过了，故本篇中不做描述。

传感器工作流程介绍

传感器软件层面的工作流程如下图所示，包括传感器初始化和测量。所有步骤都可以在通讯手册中查到，这里仅做一个简要的总结。

上电启动

上电后，需要查询是否准备好通讯。可遵循以下步骤

1. 为TMF882X供电。
2. 将Enable引脚拉高。
3. 向寄存器0xE0（ENABLE）写入0x01。写入时，主机需确保第5位和第4位的值与从设备读取的值一致。
4. 轮询ENABLE寄存器，直到读取到值0x41。
5. 读取寄存器0x00（APPID）以确定正在运行的应用程序。

传感器的启动分为冷启动和热启动，设备在以下情况下会视为冷启动：

1. 上电且ENABLE信号为高电平；
2. 电源循环或ENABLE信号保持低电平至少1毫秒后再次变为高电平。

其他复位被视为热启动。一般在使用中，都是冷启动。无论冷启动还是热启动，主机都应确保设备已准备好通信，并查询当前应用程序。

下载固件

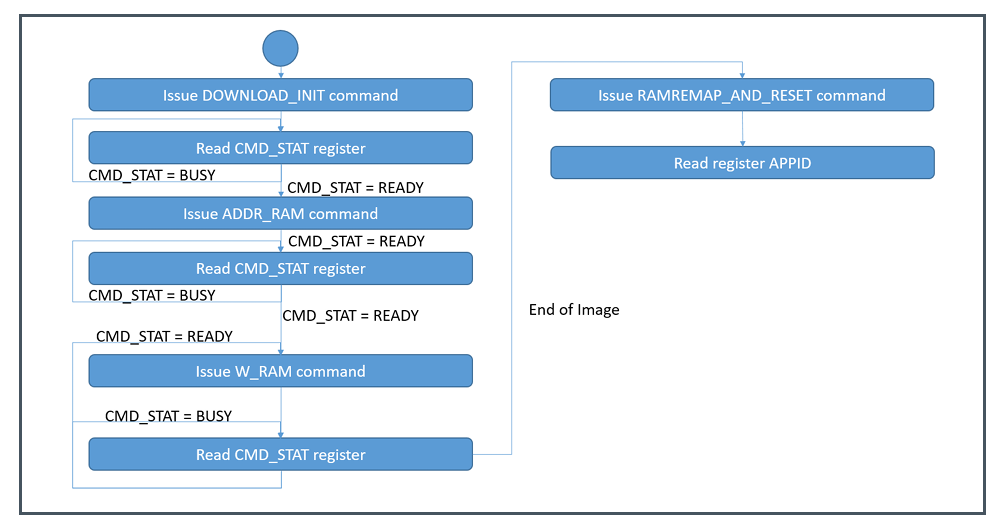
传感器上电启动完成后，通过查询寄存器0x00（APPID）来判断传感器是否处于测量状态（0x03）。如果处于测量状态，可跳过该步骤；如果不是（如0x80），则需要下载固件，下载固件的流程图如下图所示。固件文件可以从该传感器的官方介绍界面的Software栏中下载。

配置状态寄存器

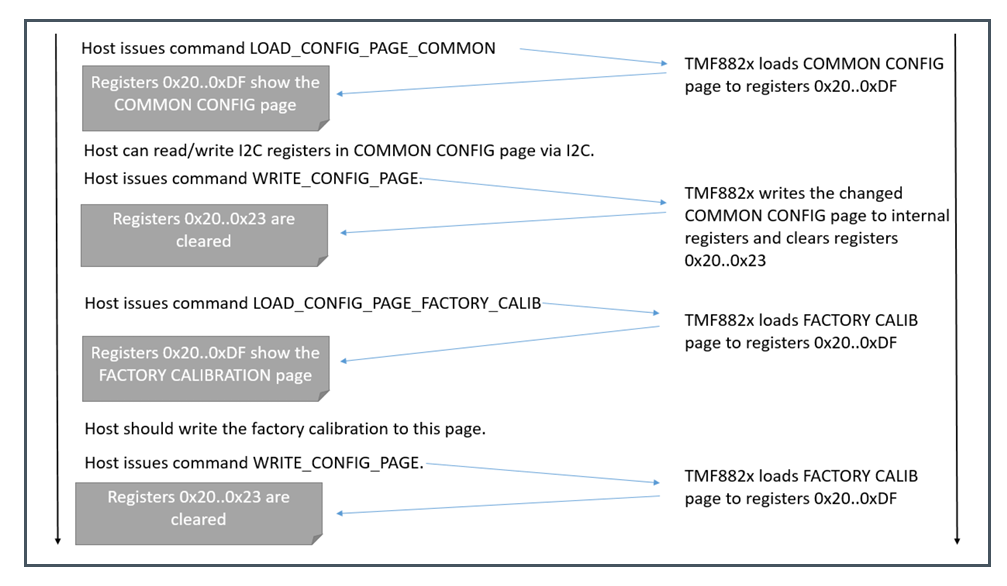
配置状态寄存器的流程图参考下图。设备在内部重新配置后，仅进行简单的完整性检查，此时配置不生效。要使配置生效，需发出MEASURE命令，此时设备会进一步检查配置的有效性。

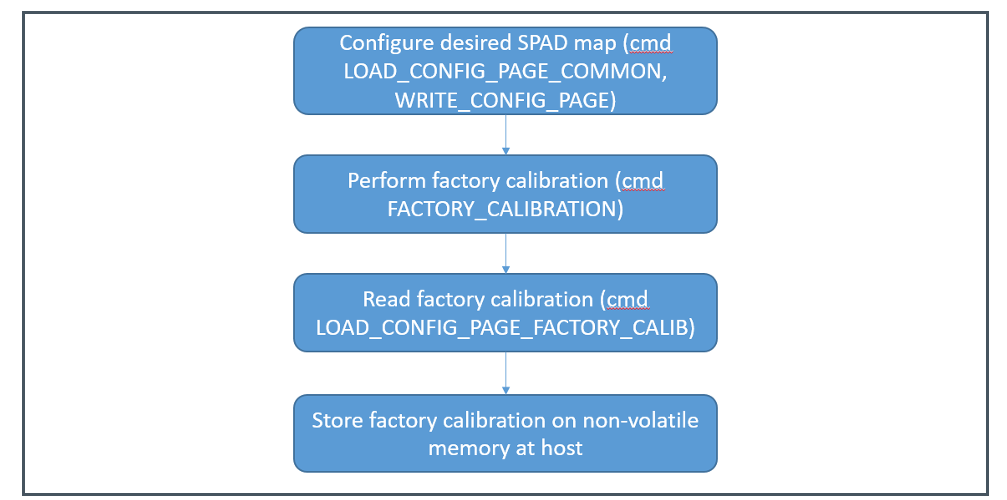
配置校准数据

配置校准数据时需要先获取获取校准数据，然后再写入传感器的配置中。如果不进行校准也可以进行测量，但未校准设备的测量结果准确性较低。如果设备缺少有效的工厂校准数据或校准与当前SPAD映射不匹配，寄存器CALIBRATION_STATUS会报告警告（0x31或0x32）。

获取校准数据时，为实现最佳性能，需设置合适的SPAD掩码、并将迭代次数设为4M后再执行算法校准（cmd_stat = 0x20）。需要将传感器嵌入最终的应用设备并安装含IR墨水的盖板玻璃。同时，校准测试需在低环境光且视场内40厘米无目标的条件下完成。加载校准数据后不会立即检查校准与SPAD映射的匹配性，只有在测量时才会进行。

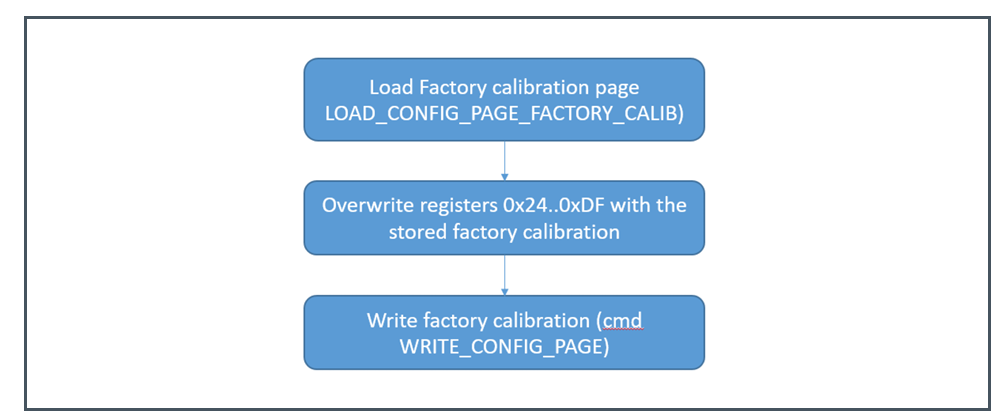
或许校准数据和加载校准数据的流程图如下图所示。

测量

设备配置和校准完成后，按以下步骤启动测量：

1. 设置INT_ENAB寄存器以启用所需中断。
2. 清除未处理中断。
3. 发送MEASURE命令启动测量。
4. 读取CMD_STAT寄存器确认命令是否被接受，返回值应为0x01，否则需检查错误。

设备接受MEASURE命令后，主机需等待INT引脚被断言或轮询INT_STATUS寄存器。读取并清除INT_STATUS后，通过I²C块读取132字节的结果数据（寄存器0x24到0xa3）。为确保读取的数据仅来自一个结果记录，必须通过I²C块请求读取结果。设备会在结果可用且I²C总线空闲时发布新结果。I²C总线空闲指没有主机对其进行读写操作。

主机可通过STOP命令停止设备，并通过读取CMD_STAT寄存器确认命令执行成功。命令执行可能需要2毫秒，期间固件会尝试关闭硬件，失败则强制关闭并返回STAT_OK。

数据计算流程

项目问题与计算工作流程图

前文已经介绍过，通过查询数据手册，可以知道传感器光学器件的物理结构和在指定SPAD掩码下的FOV。由此可以计算出每个掩码中的zone对应的法向量$F_i=(f_{ix},f_{iy},f_{iz})$，i的数量取决于SPAD掩模的选择。

通过测量，可以得到传感器沿法向量组到平面B的距离组$d_i$。

最终目的是通过$F_i=(f_{ix},f_{iy},f_{iz})$和$D_i$计算出传感器与平面B之间的距离$d$，和平面法向量与z轴之间的夹角$\theta$，和平面法向量在 XY 平面上的投影与x轴之间的夹角$\phi$。

计算工作流程图如下：

关于计算方向向量和获取测量结果的方法已在前文说明完毕，这里重点说明平面拟合和计算最终结果的方法

计算方案介绍

在这里，我使用的基于最小二乘法的平面拟合方法。最小二乘法拟合平面通过最小化数据点到拟合平面距离的平方和来确定平面的最优参数。该方法的特点如下：

• 最小二乘法通过最小化误差平方和，保证了整体误差尽可能小，而不是仅关注某些点的误差。
• 它充分利用了所有数据点的信息，将测量噪声的影响降到最低。
• 数学上，最小二乘法的解是数据点集合的“均值”平面，使拟合具有统计意义上的最优性。
• 直接利用利用矩阵运算直接导出解析解，运算效率高。

最小二乘法的原理在这里不做赘述，请自行学习。

计算方案分析

一个平面​B的方程可以表示为：

$n_{a}x+n_{b}y+n_{c}z+d_0=0$

其中，$(n_a,n_b,n_c)$是平面的法向量，$d_0$是平面方程的常数项。为了方便起见，假设$d_0=-1$，这样可以将平面方程归一化为：

$ax+by+cz-1=0$

假设已知从点$P(0,0,0)$出发沿着 9 个不同的归一化方向向量$F_i=(f_{ix},f_{iy},f_{iz})$到达平面B上的点 $Q_i$，且每个点$Q_i$到平面B的距离为$D_i$。每个观测点$Q_i$的坐标可以表示为：

$Q_i=D_i\cdot F_i=(D_i{f}_{ix},D_i{f}_{iy},D_i{f}_{iz})$

故有9个这样的点$Q_1,Q_2,...,Q_9$，每个点都在平面B上，因此可以将平面方程$ax+by+cz-1=0$应用于每个点$Q_i$，得到以下方程组：

$a\cdot (D_i{f}_{ix})+b\cdot (D_i{f}_{iy})+c\cdot (D_i{f}_{iz})-1=0$

写成矩阵的表达形式如下：

$\left[\begin{array}{ccc}{D}_1{f}_{1x}& D_1{f}_{1y}& D_1{f}_{1z}\\ D_2{f}_{2x}& D_2{f}_{2y}& D_2{f}_{2z}\\ ⋮& ⋮& ⋮\\ D_9{f}_{9x}& D_9{f}_{9y}& D_9{f}_{9z}\end{array}\right]\cdot \left[\begin{array}{c}a\\ b\\ c\end{array}\right]=\left[\begin{array}{c}-1\\ -1\\ ⋮\\ -1\end{array}\right]$

即：

$X\cdot \left[\begin{array}{c}a\\ b\\ c\end{array}\right]=Y$

根据最小二乘法，解可以通过正规方程来表示：

$\left[\begin{array}{c}a\\ b\\ c\end{array}\right]=(X^{T}X{)}^{-1}{X}^{T}Y$

由此，可以求得点P到平面B的距离$d$为：

$d=\frac{1}{\sqrt{a^2+b^2+c^2}}$

同时，夹角$\theta$与$\phi$的表达式分别为：

$\begin{array}{ccc}\theta & =& \arccos \left(\frac{c}{\sqrt{a^2+b^2+c^2}}\right)\\ \phi & =& \{\begin{array}{ccc}90^{\circ }& ,& a=0,b>0\\ 270^{\circ }& ,& a=0,b<0\\ 0^{\circ }& ,& a=0,b=0\\ \arctan \left(\frac{b}{a}\right)& ,& a\ne 0\end{array}\end{array}$

代码展示

具体说明都在注释中。

import math

def normalize_vector(v):
    """
    归一化向量
    :param v: 输入向量 (x, y, z)
    :return: 归一化后的向量 (x, y, z)
    """
    length = math.sqrt(v[0]**2 + v[1]**2 + v[2]**2)
    return (v[0]/length, v[1]/length, v[2]/length)

def calculate_normalized_vectors(A, points):
    """
    计算从点A到各点的归一化向量
    :param A: 点A的坐标 (x, y, z)
    :param points: 九个点的坐标列表 [(x1, y1, z1), (x2, y2, z2), ...]
    :return: 归一化向量列表 [(x1, y1, z1), (x2, y2, z2), ...]
    """
    normalized_vectors = []
    for point in points:
        vector = (point[0] - A[0], point[1] - A[1], point[2] - A[2])
        normalized_vector = normalize_vector(vector)
        normalized_vectors.append(normalized_vector)
    return normalized_vectors


def calculate_angle_between_planes(plane_normal):
    """
    计算向量 plane_normal 与 Z 轴和 X 轴的夹角（在 XY 平面上的投影）
    :param plane_normal: 输入向量 (x, y, z)
    :return: 向量与 Z 轴和 X 轴的夹角 [angle_z, angle_x]（单位为度）
    """
    x, y, z = plane_normal

    # 计算向量的模长
    length = math.sqrt(x**2 + y**2 + z**2)
    if length == 0:
        raise ValueError("向量长度为零，无法计算夹角")

    # 计算与 Z 轴的夹角
    cos_theta_z = z / length
    angle_z = math.degrees(math.acos(cos_theta_z))

    # 计算与 X 轴的夹角（在 XY 平面上的投影）
    if x == 0:
        if y > 0:
            angle_x = 90.0  # 向量指向 Y 轴正方向
        elif y < 0:
            angle_x = 270.0  # 向量指向 Y 轴负方向
        else:
            angle_x = 0.0  # 向量与 Z 轴重合，无 X 轴分量
    else:
        angle_x = math.degrees(math.atan2(y, x))
        if angle_x < 0:
            angle_x += 360  # 将角度转换为 0° 到 360° 范围

    return [angle_z, angle_x]

def calculate_plane_normal(F, D):
    """
    平面拟合
    :param F: 输入向量列表[[x1, yz, z1], ..., [xn,yx,zn]]
    :param D: 输入距离 [d1, ..., dn]
    :return normal_vector: 归一化的平面法向量[nx,ny,nz]
    :return z_at_origin: 平面到传感器的距离 
    """
    n = len(F)
    X = [[D[i] * F[i][0], D[i] * F[i][1], D[i] * F[i][2]] for i in range(n)]
    
    # 计算 X^T * X
    XT_X = [[sum(X[i][k] * X[i][j] for i in range(n)) for j in range(3)] for k in range(3)]
    
    # 计算 X^T * (-1)
    XT_Y = [-sum(X[i][k] for i in range(n)) for k in range(3)]
    
    # 高斯消元求解线性方程组 AX = B
    def gaussian_elimination(A, B):
        size = len(A)
        for i in range(size):
            max_row = max(range(i, size), key=lambda r: abs(A[r][i]))
            A[i], A[max_row] = A[max_row], A[i]
            B[i], B[max_row] = B[max_row], B[i]
            
            factor = A[i][i]
            for j in range(i, size):
                A[i][j] /= factor
            B[i] /= factor
            
            for k in range(i + 1, size):
                factor = A[k][i]
                for j in range(i, size):
                    A[k][j] -= factor * A[i][j]
                B[k] -= factor * B[i]

        X_res = [0] * size
        for i in range(size - 1, -1, -1):
            X_res[i] = B[i] - sum(A[i][j] * X_res[j] for j in range(i + 1, size))
        return X_res

    # 计算平面法向量 (a, b, c)
    a, b, c = gaussian_elimination(XT_X, XT_Y)
    normal_vector = normalize_vector((a,b,c))

    # 计算距离
    z_at_origin = 1/math.sqrt(a**2+b**2+c**2) if c != 0 else None

    return normal_vector, z_at_origin


# 调用示例
if __name__ == "__main__":
    vectors = [(-0.05676579, 0.07204306, -0.9957849), (0.0, 0.07215941, -0.997393), (0.05676579, 0.07204306, -0.9957849), (-0.05691368, 0.0, -0.9983791), (0.0, 0.0, -1.0), (0.05691368, 0.0, -0.9983791), (-0.05676579, -0.07204306, -0.9957849), (0.0, -0.07215941, -0.997393), (0.05676579, -0.07204306, -0.9957849)]
    distances = [192000, 192000, 199000, 192000, 179000, 192000, 190000, 193000, 194000]
    normal, z = calculate_plane_normal(vectors, distances)
    if normal[2]<0:
        normal=(-normal[0],-normal[1],-normal[2])
    print("平面法向量为: ({:.4f}, {:.4f}, {:.4f})".format(normal[0], normal[1], normal[2]))
    print("平面B的距离：")
    print("{:.4f}".format(z))

    angles = calculate_angle_between_planes(normal)
    print("向量与 Z 轴和 X 轴的夹角（在xy面的投影）分别为: [{:.2f}°, {:.2f}°]".format(
        angles[0], angles[1]
    ))

功能展示

运行main.py后，开发板会自动完成RP2040和传感器的初始化，完成后的输出如下所示：

输入1并按回车可以看到帮助：

先输入6采用默认配置，再输入8即可进行单次测量，并输出结果：

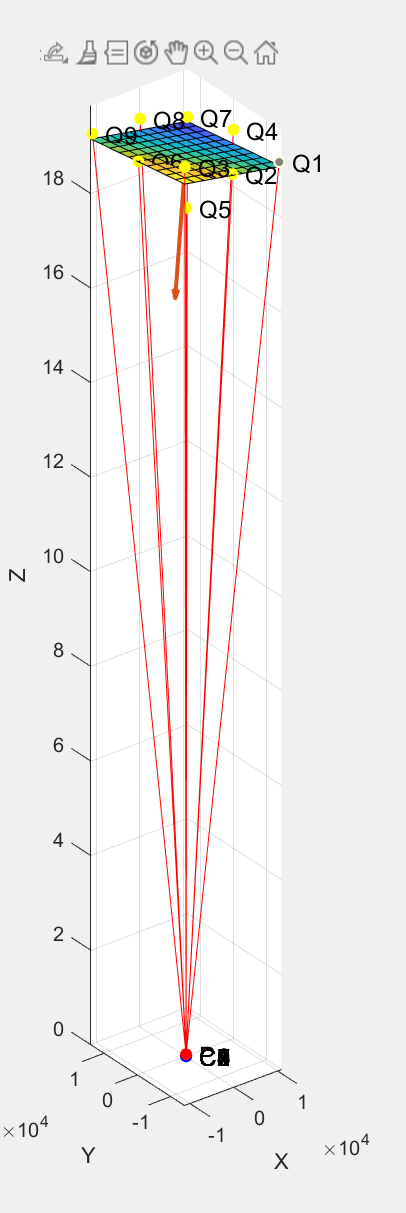
在matlab中，使用相同的数据计算得出的结果与在开发板中得到的结果一致，由此验证结果正确。

在matlab中的作图如下。其中红线即为每个zone对应的法向量所在的直线，红线的长度即为测量结果，Qn点为每个zone测量出来的点，渐变色的平面即为拟合后的平面，橙色箭头为平面的法向量。

项目中遇到的问题和解决方法

• 由于micropython没有类似numpy的数据处理库，所以关于矩阵变换的代码都得自己从零开始写
• 由于没有较为精确的测试环境，故无法验证数据的精确性，只能在大致的范围判断出正确